Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 91
A viga em balanço com perfil W360 64 feita de aço A-36 é submetida à carga mostrada na figura. Determine o deslocamento em C.
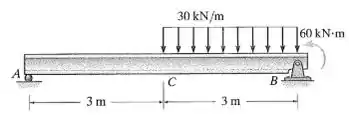
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat. Aqui vamos usar o método da superposição. Nele, vamos usar duas situações estáticas distintas, que quando sobrepostas, dão a nosssa viga fofa do enunciado.
Podemos pensar nesses dois casos aqui:
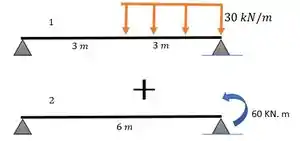
Repara que em um a gente tem só a carga distribuída e no outro só o momento.
A ideia aqui é que a gente pode separar a situação da nossa viga em situações que já são tabeladas. E depois podemos só somar os resutados. Aí evita mais continhas. Bora ver como isso fica!
Passo 2
Para esta viga com perfil , no caso 1, temos uma fórmula tabelada para o deslocamento no meio. Cê acha no apêndice C. A fórmulinha é:
Quem é quem aí? é o comprimento da viga, ou seja, . E o valor da carga, ou seja,
Passo 3
Conseguimos também fórmuinhas para o caso 2. No mesmo apêndice. A gente consegue achar a função para a deflexão:
Considerando saindo da extremidade direita da viga. O meio vale .
Já vimos que e é o momento concentrado no caso 2
Passo 4
Podemos somar o que a gente achou para o caso 1 e para o caso 2, pelo príncipio da superposição.
Sendo valores tabelados:
Essa deflexão está para baixo, bele?