Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 104
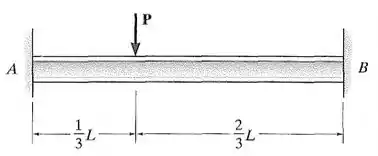
Determine as reações nos apoios e ; em seguida, trace os diagramas de força cortante e momento fletor. é constante. Despreze o efeito da carga axial.
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat.
Nossa estrutura é hiperestática e só tem forças verticais. Aí a gente vai achar as reações de apoio pela linha elástica. Olha nosso DCL:
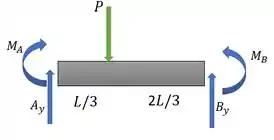
A ideia aqui é achar as equações das linhas elásticas em função das reações em ou . E achar a essas reações pelas condições de contorno. Depois é usar as equações de equilíbrio para achar as reações que faltarem. Vai ser bonito. Vem ver como fica!
Passo 2
Para determinarmos as forças de reação, vamos utilizar a equação do momento em , e achar as reações nele em função de e , temos:
Passo 3
Com isso, podemos determinar a função de momento fletor pela Função de Macaulay:
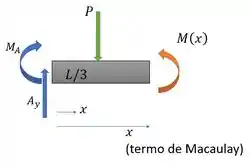
Essa função representa que para , esse termo zera. E para , esse termo vale . Aí não precisamos escrever uma equação para cada seção.
E então, pelo método da integração, vamos obter a equação da linha elástica. Fica assim:
Passo 4
Para determinarmos as incógnitas restantes, temos que utilizar as seguintes condições de contorno:
Para
Isso porque temos um engaste. Nele a deflexão e a inclinação zeram.
Logo:
Para
Isso porque temos outro engaste:
Para (também por causa do engaste):
Assim, igualando as equações e , vamos obter as reações nos apoios:
Passo 5
Voltamos nas equações de equilíbrio para achar as reações em :
Passo 6
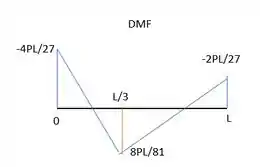
Por fim, temos que a função do momento fletor vai ser:
Assim, podemos esboçar o diagrama de momento fletor:
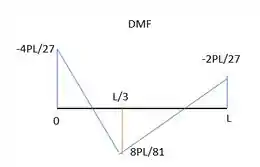
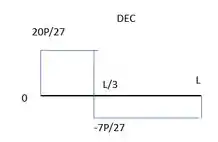
Para esborçar o do cortante a gente segue o caminho das forças concentradas. Em subimos , depois ficamos constantes até a posição de , onde descemos . E depois ficamos constantes até , onde subimos . Ficamos assim:
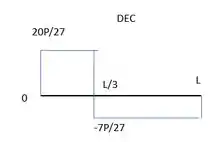
Resposta
