Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 107

Determine as reações ao momento nos apoios A e B. EI é constante.

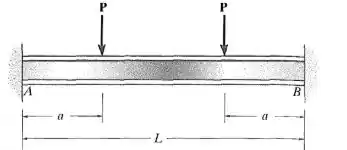
Passo 1

Fala aí pessoal, partiu mais um problema de resmat. Este problema pede as reações de apoio da estrutura hiperestática. Existem inúmeros métodos para resolver o problema, eu vou usar a Equação de Macaulay. Primeiro, vamos fazer o somatório de momentos em B:

∑ M B = 0 → P L + M A - A y L - M B = 0

As equações do momento são:

M x 1 = A y x 1 - M A → 0 ≤ x 1 ≤ a

M ( x 2 ) = A y x 2 - P x 2 + P a - M A → a ≤ x 2 ≤ L - a

Sabemos que:

E I d v 2 d x 2 = M x

Integrando-se duas vezes as equações do momento, temos:

E I v 1 = A y 6 x 1 ³ +   C 1 x 1 + C 2

E I v 2 = A y 6 x 2 ³ - P 6 x 2 ³ + P a 2 x 2 ² +   C 3 x 2 + C 4

Para a determinação das constantes, temos que aplicar as condições de contorno. As condições de contorno são:

x 1 = 0 → v 1 = 0  

x 2 = L 2 → d v 2 d x 2 = 0  

Logo:

C 1 = 0

C 2 = 0

C 3 = - A y L 2 8 + P L 2 8 - P a L 2 + M A L 2

C 4 = 0

Passo 2

Agora vamos utilizar alguns pontos para determinar as reações:

x 1 = a   e   x 2 = L - a → d v 1 d x 1 = - d v 2 d x 2

x 1 = x 2 = a → d v 1 d x 1 = - d v 2 d x 2

Logo:

M A = P a L L - a

M B = P a L L - a

Resposta

M A = P a L L - a

M B = P a L L - a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga está sujeita à carga mostrada na figura. Determine a equação da linha elástica. EI é constante.
Determine a equação da linha elástica. Especifique a inclinação em A
Determine a reação no apoio móvel e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados na figura.
Determine a reação em A e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados nas figuras.
Para a viga e o carregamento mostrados na figura, determine ( a ) a reação em C , ( b ) a deflexão no ponto B . Utilize E = 29 × 10 6p s i .