Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 80
Determine a resultante das três forças atuando no olhal. Ache também o módulo de e o ângulo que a resultante faz com o eixo .
Passo 1
E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?
Prestem bastante atenção que essa questão é relativamente rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não se perca no meio do caminho. Pois bem, primeiro de tudo vamos decompor nossas forças de modo que encontraremos
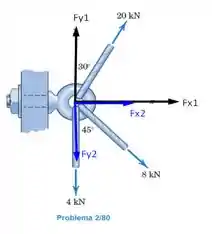
Agora, conseguimos achar as componentes da nossa resultante que serão dadas por
Passo 2
Com isso, conseguimos calcular o módulo da nossa resultante que será dado por
Por fim, para concluirmos nosso exercício basta encontrarmos o ângulo basta fazermos
Pronto! Está resolvido nosso exercício.
Resposta
Exercícios de Livros Relacionados
A inclinação da força F de 4,8k N está especificada como mostrado na figura. Expresse F como um vetor, em termos dos vetores unitáriosi e j .
A força F em um módulo de 800N . Expresse F como um vetor, em termos dos vetores unitáriosi e j . Identifique os componentes escalares de F em x e y .
No projeto de um mecanismo de controle é determinado que a barra A B transmite uma força P de 260N à manivela B C . Determine os componentes escalares x e y de P .
O módulo da força F é 6 00N . Expresse F como um vetor, em termos dos vetores unitáriosi e j . Identifique os componentes escalares e vetoriais de F .
Os dois elementos estruturais, um sob tração e o outro sob compressão, exercem as forças indicadas no nó O . Determine o módulo da resultante R das duas forças e o ângulo θ que R faz com o eixo x posi