Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 93
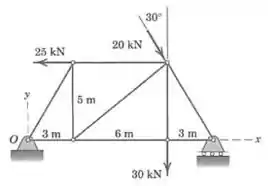
Determine a resultante das três forças atuando na treliça simples. Especifique os pontos sobre os eixos e através dos quais deve passar.
Passo 1
O primeiro passo é calcular a força resultante. Para isso precisamos fazer a soma vetorial de todas as forças da figura:
E então:
Passo 2
Agora precisamos calcular o momento total dessas forças em relação ao ponto :
E então o momento total é:
Passo 3
A força resultante precisa gerar exatamente o momento que acabamos de calcular. Vamos escrever esse momento em forma vetorial, sabemos que como a rotação acontece no plano da página o momento deve apontar na direção perpendicular a esse plano:
E dependendo da posição do ponto em que é aplicado, o torque gerado por é:
Onde , então:
Vamos resolver esse produto vetorial usando a notação matricial (você pode usar outro método se preferir):
E então a nossa equação fica da seguinte forma:
E para encontrar os pontos sobre os eixos através dos quais deve passar só precisamos substituir os seguintes valores:
Resolvido!
Resposta
A força resultante é e os pontos sobre os eixos são e .