Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 96
A roda traseira de um automóvel de tração dianteira que está acelerando para a direita está submetida às cinco forças e ao momento mostrado. As forças e são forças transmitidas pelo eixo à roda, é a força exercida pela superfície da estrada no pneu, é a força normal de reação exercida pela superfície da estrada e é o peso do conjunto pneu/roda. O momento é devido à fricção do mancal. Determine e localize a resultante do sistema.
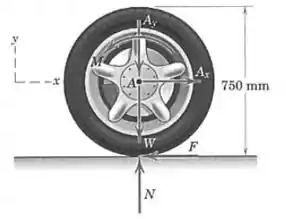
Passo 1
Vamos começar escrevendo todas as forças em forma vetorial:
E agora podemos calcular a força resultante somando esses cinco vetores:
E agora vamos calcular o momento dessas forças em relação ao ponto . Essa é conta é mais fácil do que parece, porque as forças , e têm linhas de ação que passam pelo próprio ponto , então a única força que produz momento é , além do próprio momento :
Passo 2
Nosso objetivo é determinar a localização da resultante que calculamos.
Para fazer isso só temos que encontrar a distância em relação ao centro que produza o mesmo momento que calculamos acima:
Sabemos que a direção é horizontal, porque o vetor só tem uma componente no eixo :
Como a força aponta no sentido positivo, e nós vimos que o momento total é negativo (rotação no sentido horário). Isso quer dizer que tem que ser aplicada acima do ponto , se não teríamos rotação no sentido anti-horário.
Resposta
A força resultante é , e deve ser aplicada a uma distância acima do ponto .