Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 91
Para essa viga, as especificações de projeto para o encaixe em dependem do módulo e da posição das cargas aplicadas. Represente a resultante das três forças e do momento por uma única força em e por um momento . Especifique o módulo de .
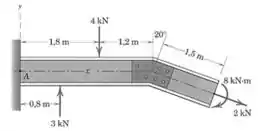
Passo 1
Começamos calculando a força resultante sobre o sistema. Na direção horizontal temos apenas uma componente da força de :
E na direção vertical temos que considerar também as duas forças mais à esquerda:
E então a força resultante é:
E então o módulo de já pode ser calculado:
Passo 2
Agora vamos supor que essa força seja aplicada sobre o ponto . Nesse caso, para que o efeito sobre o sistema seja o mesmo, precisaremos aplicar um momento igual ao que as forças (e o momento de ) produziam inicialmente:
E então o momento que teríamos que “repor” é (que favorece a rotação no sentido horário).
Resposta
A força resultante é , tem módulo e o momento necessário é (sentido horário).