Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 93

Duas polias estão submetidas às forças trativas das correias, como mostrado. Se a resultante dessas forças passa pelo centro , determine , o módulo de e o ângulo anti-horário que faz com o eixo .

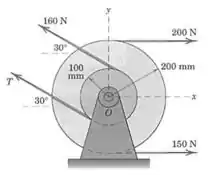
Passo 1

Se a força resultante passa pelo ponto , isso quer dizer que o momento total em relação a é:

Podemos usar essa condição para calcular .

Vamos começar calculando os momentos das forças de e :

Agora os momentos de e da força de :

E então o momento total em relação a é:

Como esse momento precisa ser nulo:

Passo 2

Agora vamos calcular a força resultante . É uma boa ideia escrever cada uma das forças em forma vetorial:

E agora podemos calcular :

E então o módulo da força é:

Passo 3

E conhecendo as duas componentes de podemos calcular o ângulo que o vetor forma com a horizontal:

Então:

Resposta

, e .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As direções dos dois vetores de empuxo de um avião experimental podem ser variadas independentemente, dentro de certos limites, desde a direção convencional à frente. Para a configuração de empuxo mos

Substitua as três forças atuando no tubo dobrado por uma única força equivalente R → . Determine a distância x a partir do ponto O até o ponto no eixo x pelo qual passa a linha de ação de R → .

Um avião comercial com quatro turbinas a jato, cada uma produzindo um empuxo à frente de 90k N , estpa em um vôo de cruzeiro, estacionário, quando o motor número 3 falha repentinamente. Determine e lo

Na posição em equilíbrio mostrada, a resultante das três forças atuando na haste dobrada passa pelo mancal O . Determine a força vertical P → . O resultado depende de θ ?

A polia e a correia em V presa a ela estão girando no sentido anti-horário e estão submetidas à carga de 1600N , devida aos dentes da engrenagem, e aos esforços trativos de 800N e 450N na correia em V