Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 82
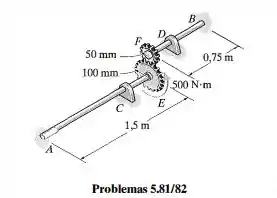
Determine a rotação da engrenagem em no Problema 5.81.
Passo 1
Oi, pessoal! Tudo bem? Espero que sim! Se não, vai ficar!!
O objetivo da questão é determinar a rotação da engrenagem em , ou seja, . Para isso realizaremos os mesmos passos para a questão anterior, se você já a fez pule para o passo .
O que nos foi disponibilizado:
Aço A-36, portanto, .
Vamos logo adiantar e determinar o momento polar de inércia ();
Passo 2
Devemos realizar o somatório dos momentos para determinar os torques desejados. Para isso vamos fazer o somatório dos torques em ambos os eixos.
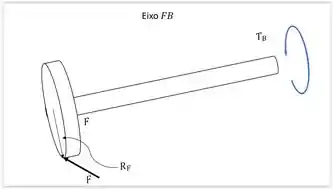
Agora em relação ao outro eixo;
Passo 3
Para determinar podemos relacionar os ângulos de torção em e com os raios das engrenagens, com isso temos:
Resolvendo o sistema temos:
Passo 4
Como já temos todos os dados, basta calcular o valor de .
O ângulo de torção é determinado por;