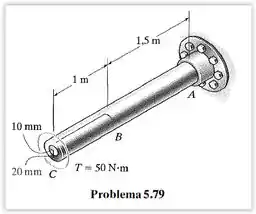
O eixo é composto por uma seção maciça de aço e uma porção tubular feita de aço com núcleo de latão. Se o eixo estiver preso a um apoio rígido e for aplicado um torque a ele em , determine o ângulo de torção que ocorre em e calcule a tensão de cisalhamento máxima e a deformação por cisalhamento máxima no latão e no aço. Considere , .

Efetuando o somatório dos momentos que atuam no eixo, temos:

Quando o eixo for submetido aos torques, o ângulo de torção do aço e do latão no segmento será o mesmo, pois nesse intervalo os materiais estão concêntricos, isso é, o latão e o aço estão presos e só podem rotacionar juntos, por isso, o ângulo de torção será o mesmo.

Em que, momento polar de inércia, , para o eixo é dado por:

E para o tubo:

Podemos cortar os termos que são iguais nos dois membros, já que . Substituindo e simplificando, temos:

Substituindo na equação que chegamos fazendo o somatório dos momentos, temos:

Vamos calcular agora o ângulo de torção em .

Como temos aço em seções diferentes, vamos escrever:

Convertendo para graus:

Aqui ficamos diferentes do gabarito, mas tá certinho, ok?

Para encontramos a tensão de cisalhamento máxima usamos:

A tensão máxima no aço vai ocorrer no segmento CB que é tubular (menor área causa maior tensão para um mesmo carregamento). Calculando:

No latão, a tensão máxima é:

Último passo, calcular a deformação por cisalhamento nos dois materiais. Ela é dada por:

Como as tensões no material permanecem abaixo dos limites de proporcionalidade e elasticidade (Lei de Hooke), podemos fazer:

Para o aço:

Para o latão: