Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 71
O eixo de aço A-36 tem diâmetro de e está sujeito aos carregamentos distribuídos e concentrados mostrados. Determine a tensão de cisalhamento máxima absoluta no eixo e construa um gráfico para o ângulo de torção do eixo em radianos em relação a .
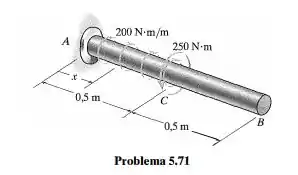
Passo 1
Oi, galerinha! Tudo joia com vocês?
O problema pede a tensão máxima de cisalhamento no eixo e o gráfico para o ângulo de torção do eixo em radianos em relação a . A a tensão de cisalhamento é dada por:
E o ângulo de torção por:
Como o eixo não apresenta mudança na sua seção transversal, o raio e o momento polar de inércia serão constantes. Sendo assim, a tensão máxima dependerá somente do torque, logo onde o torque for máximo é onde ocorrerá a máxima tensão de cisalhamento.
O mesmo vale para elaborar o gráfico, visto que esse só dependerá do torque já que as outras são constantes.
Temoss como dados:
Aço A-36, portanto,
Só com os dados iniciais é possível calcular o momento polar de inércia da seção circular da haste:
Passo 2
Visto que a questão gira em torno do torque (trocadilho intencional), temos que determinar logo a função que descreve o torque no eixo. Para isso, vamos dividir o eixo em duas partes e .
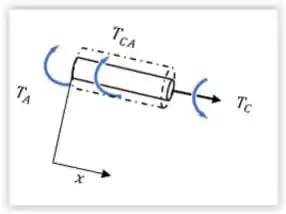
Seção :
Já conhecemos o valor de , falta determinar o valor do toque total ocasionado pelo carregamento e o valor do torque de reação no ponto . O torque total do carregamento é dado pelo carregamento multiplicado pelo comprimento de onde ele está sendo aplicado:
Como o sistema está em repouso, logo:
Agora partindo para seção :
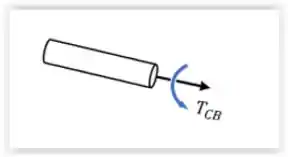
Seção :
Realizando um somatório de torques, vemos que não existe um torque na secção logo;
Passo 3
Agora vamos determinar o torque que irá produzir o ângulo de torção na seção. Como vimos que não ocorre torque a partir do ponto vamos elaborar uma equação que rege o torque na primeira parte do eixo:
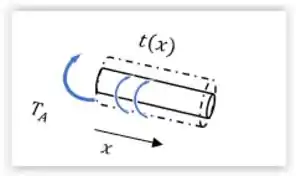
Podemos ver que o torque resultante será igual a soma do com a parcela gerada pelo carregamento:
O torque máximo ocorrerá quando for igual à .
Passo 4
Tudo determinado. Agora é só partir para o abraço!
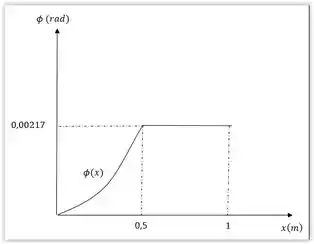
Função que descreve o ângulo de deformação:
E por fim, elaborar o gráfico. Lembrando que a partir do ponto não tem torque, então o ângulo de torção não varia na seção .
