Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 77
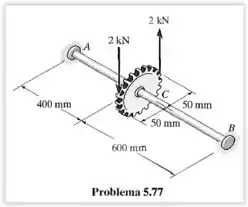
O eixo é feito de aço-ferramenta L2, tem diâmetro de e está preso em suas extremidades e . Se for submetido ao conjugado, determine a tensão de cisalhamento máxima nas regiões e .
Passo 1
Olá, pessoal! Tudo bem?
Vamos começar anotando os dados que o enunciado nos forneceu:
Aço-ferramenta L2, portando,
Analisaremos agora diagrama de corpo livre:
Na engrenagem , tem duas forças de agindo no sentido anti-horário. Então, temos que:
Fazendo o somatório dos momentos, temos:
O eixo está engastado em e , então:
Substituindo:
Portanto:
Passo 2
Para encontramos a tensão de cisalhamento máxima usamos:
Em que é o raio e o momento polar de inércia, , é dado por:
Para o segmento ,
Para o segmento ,
Resposta
Exercícios de Livros Relacionados
O eixo cheio AB tem diâmetro d s = 1.5i n , e é feito de aço com G = 11,2X 10 6 psi e τ a l l = 7 psi, enquanto a luva CD é feita de latão com G=5,6 x 10 6 psi e τ a l l = 7 ksi. Determine o maior âng
Três eixos se seção transversal cheia são conectados pelas engrenagens A e B mostradas. Sabendo que G = 77,2 GPa, determine o ângulo de torção entre (a) A e B (b) A e C.
(a) Para o eixo de alumínio mostrado G = 27G P a , determine o torque T 0 que provoca um ângulo de torção de 2° e (b) o ângulo de torção provocado pelo mesmo torque T 0 em um eixo cilíndrico cheio de
A barra de alumínio A B G = 27G P a está ligada a barra de latão B D G = 39G P a . Sabendo que a parte CD da barra de latão é vazada e tem um diâmetro interno de 40 mm, determine o ângulo de torção em
No Problema 3.114, determine o ângulo de torção permanente da barra.