Determine o sistema força-binário equivalente na origem para cada um dos três casos de forças sendo aplicadas nas arestas de uma placa quadrada de lado
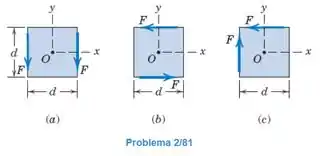
Passo 1
E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?
Prestem bastante atenção que essa questão é relativamente rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não se perca no meio do caminho. Pois bem, o procedimento para cada um dos itens será encontrar a resultante e o binário para cada uma das situações em relação ao ponto . Sendo assim, para o primeiro caso nós vamos ter
Adotando o sentido anti-horário como positivo vamos ter para o momento
Passo 2
Procedendo de igual maneira, para o segundo caso, vamos ter
Já para o momento teremos
Passo 3
Para o último item também procederemos igual aos itens anteriores, então, teremos
Agora para o momento nós teremos
Pronto, tá resolvido nosso exercício.