Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 27

Determine a tensão de cisalhamento nos pontos B e C localizados na alma da viga de fibra de vidro.

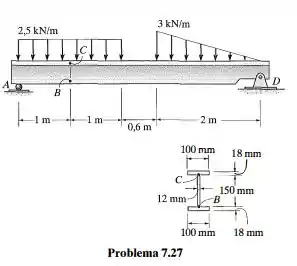
Passo 1

Vamos começar calculando as reações de apoio:

Aplicando as equações de equilíbrio:

∑ M D = 0 ⇒ - R A ⋅ 4,6 + 2,5 ⋅ 2 ⋅ 3,6 + 3 ⋅ 2 2 ⋅ 2 ⋅ 2 3 = 0

R A = 4,78   k N

∑ F y = 0 ⇒ R A - 2,5 ⋅ 2 - 3 ⋅ 2 2 + R B = 0

R B = 3,22   k N

Passo 2

O esforço na seção desejada é:

∑ F y = 0 ⇒ R A - 2,5 ⋅ 1 - V = 0

V = 2,28   k N

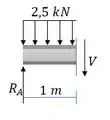
Passo 3

Agora vamos determinar o momento de inércia:

I = 100 ⋅ 150 + 18 + 18 3 12 - 100 ⋅ 150 3 12 + 12 ⋅ 150 3 12

I = 28873800   m m 4

Passo 4

Agora vamos calcular o momento estático. Perceba a viga é perfeitamente simétrica. Da mesma forma, os pontos B e C são simétricos. Isso quer dizer que o momento estático e a tensão sobre eles é a mesma.

Q B = 18 ⋅ 100 ⋅ 84

Q B = 151200   m m 3

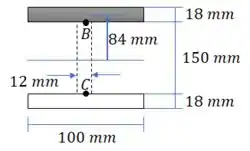
Passo 5

Agora aplicamos a equação do cisalhamento:

τ B = V Q B I t

τ B = 2,28   k N ⋅ 151200   m m 3 28873800   m m 4 ⋅ 12   m m

τ B = 0,995   M P a

Resposta

τ B = 0,995   M P a

τ C = 0,995   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é feita de um material cerâmico cuja tensão de flexão admissível é σ a d m = 5 MPa e tensão de cisalhamento τ a d m = 2,8 MPa. Determine a largura b da viga, se a altura for h=2b.
A viga T de aço em balanço foi montada com duas chapas soldadas como mostra a figura. Determine as cargas máximas P que podem ser suportadas com segurança pela viga, se a tensão de flexão admissível f
A viga é construída com duas tábuas presas uma à outra na parte superior e na parte inferior por duas fileiras de pregos espaçados de 150 mm. Se cada prego puder suportar uma força de cisalhamento de
Uma viga extrudada tem a seção transversal mostrada na figura é uma parede de espessura uniforme de 3 ymm. Para força cortante vertical de 10 kN, determine (a) o tensão de cisalhamento no ponto A, (b)
Determine a força de cisalhamento máxima V que a escora pode suportar se a tensão de cisalhamento admissível para o material for τ a d m = 40M P a