Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 17
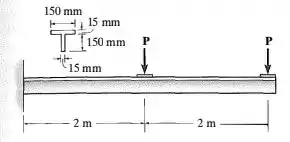
A viga T de aço em balanço foi montada com duas chapas soldadas como mostra a figura. Determine as cargas máximas P que podem ser suportadas com segurança pela viga, se a tensão de flexão admissível for σ = 170 Mpa e a tensão de cisalhamento for τ = 95MPA.
Passo 1
Antes de tudo, vamos olhar a nossa viga:
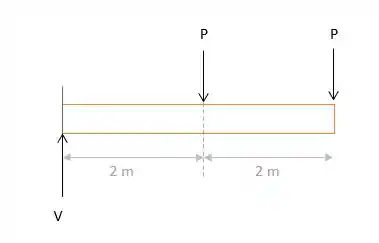
Pelo equilíbrio estático, temos que o somatório de forças e o somatório dos momentos são iguais a zero, lembrando que temos uma força e um momento de reação no lado da viga que está preso.
Agora, com os valores de todas as forças em mãos, podemos visualizar os esforços na viga.
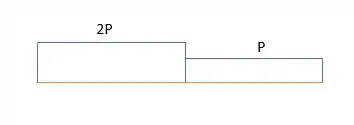
Assim, podemos ver que e
Passo 2
Então, precisamos dar uma olhada na seção transversal:
Primeiro, vamos calcular (altura do eixo neutro) dessa seção, divindindo em duas áreas (a mais clara e a mais escura) como na figura:
Dessa forma, lembrando do teorema dos eixos paralelos, podemos calcular o momento de inércia:
, sendo d = a distância até
Sendo c, a maior distância até o eixo neutro, igual a 116,25 mm e , então:
Passo 3
Precisamos conferir se a viga não irá cisalhar!
Tá lembrando que lá em cima dissemos que V=2P? Então olha os dados que já temos:
Para calcular Q, vamos voltar a nossa seção:
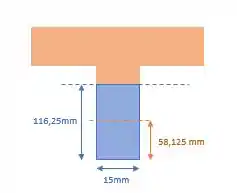
Q é calculado como a multiplicação da área em azul (área até a linha neutra) pela distância do centroide dessa área até a linha neutra. Ou seja:
³
Voltando para o cálculo da tensão de cisalhamento:
Ou seja, a tensão não irá cisalhar a viga. Resultado: essa condição está OK.
Resposta
P = 2,8kN