Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 62
Determine o torque M que deve ser aplicado à alça do parafuso para começar a mover o bloco de 100 lb para cima na inclinação de 15 ∘. O coeficiente de atrito estático entre o bloco e a inclinação é 0,50, e o parafuso de rosca única tem roscas quadradas com um diâmetro médio de 1 pol. E avança 0,4 pol. Para cada volta completa. O coeficiente de atrito estático das roscas também é 0,50. Despreze o atrito na pequena junta esférica A.
Passo 1
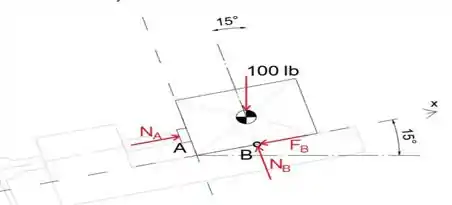
Primeiro, vamos desenhar o diagrama de corpo livre do bloco, a fim de determinar a força necessária para mover o bloco
Uma vez que o bloco está começando a se mover, a força de atrito em B é a força de atrito máxima
Passo 2
Equacionando a soma das forças na direção x e y a zero, determinaremos a força NA necessária para mover o bloco
Agora calcularemos a força de fricção
Passo 3
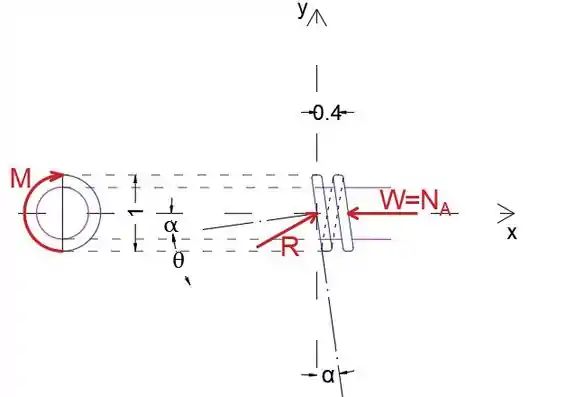
Equação do momento de equilíbrio
(1)
Em que X é a força axial aplicada no parafuso
R é o raio
α é o ângulo que a rosca faz com o eixo y, uma vez que a rosca se move 0,4 por revolução, e a circunferência de um círculo é 2rπ, podemos determinar α
Podemos determinar o ângulo, uma vez que sabemos o coeficiente de fricção
Finalmente, colocando todos os valores conhecidos na equação (1), vamos determinar M