Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 85

Repita Prob. 6/84 para o caso de abaixamento do cilindro de massa m a uma velocidade constante.

Passo 1

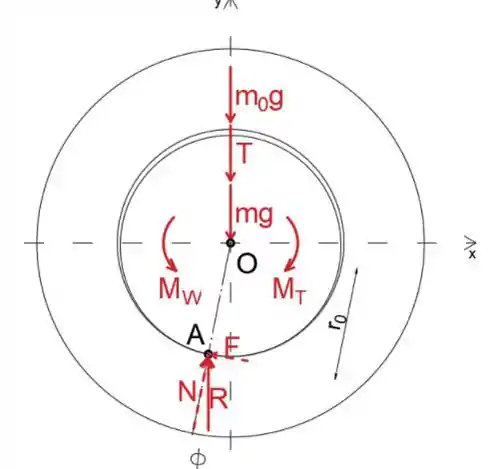
Primeiro, vamos substituir o peso e a tensão por dois sistemas de força-acoplamento atuando no ponto O

Enquanto os momentos que o peso da carga e da tensão T fazem sobre o ponto O são

M w = m g ⋅ k r                     ( 1 ) M T = T ⋅ r                                 ( 2 )

Passo 2

A seguir, desenharemos o diagrama de corpo livre do eixo

Para que o sistema esteja em equilíbrio, a força resultante deve ser vertical

Como malos resultante com o ângulo de força normal ϕ, podemos escrever a força de atrito F como

F = R s i n ⁡ ϕ

Vamos substituir sin ϕ por μ para obter

F = μ R (3)

Observe que, para levantar o peso, a polia deve girar no sentido horário, o que significa que a força de atrito irá girá-la na direção oposta e que o peso da polia menor também atua no rolamento

Passo 3

Equacionando a soma das forças no eixo y a zero, determinaremos a força de reação R

∑   F y   = 0 R   - m g - T - m 0 g = 0 R   = m + m 0 g + T                                                                       ( 4 )

Vamos igualar a soma dos momentos sobre o ponto O a zero

∑ M O = 0

- M W - F ⋅ r 0 + M T = 0

Vamos substituir MW, MT e F pelas expressões (1), (2) e (3), respectivamente

- m g ⋅ k r - μ R + T ⋅ r = 0

Substituiremos R pela expressão (4)

- m g + k r - μ m + m 0 g + T ⋅ r 0 + T ⋅ r = 0 - m g ⋅ k r - m + m 0 g ⋅ μ ⋅ r 0 - T ⋅ μ ⋅ r 0 + T ⋅ r = 0 - m g ⋅ k T - m + m 0 g ⋅ μ ⋅ r 0 + T r - μ ⋅ r 0 = 0

Finalmente, vamos substituir m, m0, k μ, r e r0 por seus valores

T = 50 ⋅ 9.81 ⋅ 0.5 ⋅ 300 - ( 50 + 30 ) ⋅ 9.81 ⋅ 0.15 ⋅ 25 300 + 0.15 ⋅ 25

T = 232.53 N

Resposta

T = m g ⋅ k r + m + m 0 g ⋅ μ ⋅ r 0 r - μ ⋅ r 0

T = 232.53 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de aço de 1,2 toneladas é movida sobre uma superfície nivelada usando uma série de roletes com diâmetro de 30m m , para os quais o coeficiente de resistência a rolamento é 0,4m m no solo e 0,2m
O carrinho, juntamente com a carga, pesa 750N( ≈ 75k g ) . Se o coeficiente de resistência ao rolamento é a = 0,75m m , determine a força necessária para puxar o carrinho com velocidade constante.
O rolo compressor tem uma massa de 80k g . Se o braço B A for mantido a um ângulo de 30 ° da horizontal e o coeficiente de resistência ao rolamento para o cilindro for 25m m , determine a força P nces
O cilindro está sujeito a uma carga que tem um peso W . Se o coeficiente de resistência ao rolamento para as superfícies superior e inferior do cilindro forem a A e a B , respectivamente, mostre que u
Determine a força P necessária para superar a resistência ao rolamento e suportar o cilindro de 50k g se ele rolar para baixo no plano inclinado com velocidade constante. O coeficiente de resistência