Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 13
Determine a tração no cabo que dará ao bloco de uma aceleração constante de para cima no plano inclinado.
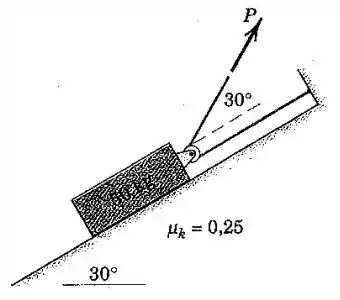
Passo 1
Galera, bora lembrar que, quando um bloco de massa está num plano inclinado de , ele terá uma componente da força peso na direção do movimento, cujo módulo é:
E a outra componente da força peso, perpendicular a esta, terá módulo:
Na mesma direção de , age uma componente da tração , cujo módulo é:
onde é o ângulo formado pelo cabo. Como no nosso problema teremos , deixaremos assim:
Uma outra força importante aqui é a normal, com módulo , que age na mesma direção de e de . Para descobrir o seu valor em termos de , , e , repare que o bloco não voa nem afunda no plano inclinado, o que significa que existe equilíbrio de forças nessa direção, ou seja:
Passo 2
Na mesma direção da componente do peso , também atuam a outra componente da tração , em sentido contrário a , cujo módulo é
e mais uma tração , devido à corda passar por uma polia, no mesmo sentido de .
Por último, também atua a força de atrito cinético , que sempre tem sentido contrário ao movimento. No nosso caso, queremos que o bloco suba o plano inclinado, então a força de atrito terá sentido descendo o plano, isto é, no mesmo sentido de . Seu módulo é dado por:
Substituímos o módulo da força normal já obtido anteriormente:
Assim, para que tenhamos uma aceleração constante para cima no plano inclinado, devemos ter, pela Segunda Lei de Newton:
Passo 3
Agora vamos substituir todos os valores possíveis na última equação obtida, a fim de obter o valor da tração :