Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 117

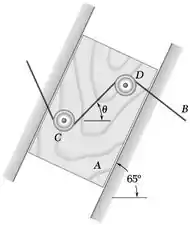
À medida que o bloco deslizante A se movimenta para baixo a uma velocidade de 0,5 m/s, a velocidade em relação a A da porção da correia B entre as polias esticadoras C e D é vCD/A = 2 m/s θ . Determine a velocidade da porção CD da correia quando (a) θ = 45°, (b) θ = 60°.

Passo 1

E ai gurizada tudo certo? O enunciado pede que a gente encontre a velocidade da porção CD da correia quando (a) θ = 45°, (b) θ = 60°.

v C D = v A + v C D / A

onde

v A = 0.5   m / s - cos ⁡ 65 ° i - sin ⁡ 65 ° j

= 0.21131   m/s i - 0.45315   m/s j

v C D / A = 2   m/s cos ⁡ θ i + sin ⁡ θ j

Então

v C D = - 0.21131 + 2 cos ⁡ θ   m/s i + - 0.45315 + 2 sin ⁡ θ   m/s j

Passo 2

  1. Nós temos

    2. v C D = - 0.21131 + 2 cos ⁡ 45 ° i + - 0.45315 + 2 sin ⁡ 45 ° j

    = 1.20290   m/s i + 0.96106   m/s j

    Passo 3

  2. Nós temos

v C D = - 0.21131 + 2 cos ⁡ 60 ° i + - 0.45315 + 2 sin ⁡ 60 ° j

= 0.78869   m/s i + 1.27890   m/s j

Resposta

a )   v C D = 1.540   m/s     38.6 °

b )   v C D = 1.503   m/s     38.3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula é lançada verticalmente para cima em um campo gravitacional constante com velocidade inicial v 0 . Demonstre que se existir uma força de retardo proporcional ao quadrado da velocidade in
Repita o Exemplo 2.4 efetuando um cálculo no computador para resolver a equação 2.22. Use os valores a seguir: m = 1 k g , v 0 = 10 m / s , x 0 = 0 e k = 0,1 s - 1 . Elabore gráficos de v versus t , x
Uma partícula de massa m desliza para baixo sobre um plano inclinado sob a influência da gravidade. Se o movimento estiver sujeito a uma força resistiva f = k m v 2 , demonstre que o tempo necessário
Considere um projétil disparado verticalmente em um campo gravitacional constante. Para as mesmas velocidades iniciais, compare os tempos necessários para que o projétil alcance sua altura máxima (a)
Uma partícula de massa m = 1k g está sujeita a uma força unidimensional F t = k t e - α t , onde k = 1 N s e α = 0,5s - 1 . Se a partícula estiver inicialmente em repouso, calcule e elabore um gráfico