Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 112

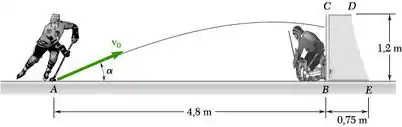
A velocidade inicial v0 de um disco de hockey é de 168 km/h. Determine (a) o maior valor (menor que 45°) do ângulo α que o disco entrará na rede e (b) o tempo correspondente necessário para o disco atingir a rede.

Passo 1

Primeira nota

v 0 = 105   mi/h = 154   ft/s

e

v x 0 = v 0 cos ⁡ α = 154   ft/s cos ⁡ α

v y 0 = v 0 sin ⁡ α = 154   ft/s sin ⁡ α

Passo 2

  1. Movimento horizontal. (Uniforme)

    2. x = 0 + v x 0 t = 154 cos ⁡ α t

    Na saída da rede,

    x = 16   ft

    Então

    16 = 154 cos ⁡ α t

    ou

    t entrar = 8 77 cos ⁡ α

    Movimento vertical. (Movimento uniformemente acelerado)

    y = 0 + v y 0 t - 1 2 g t 2

    = 154 sin ⁡ α t - 1 2 g t 2             ( g = 32.2   ft/ s 2 )

    Na saída da rede,

    y frente = 154 sin ⁡ α t entrar - 1 2 g t entrar 2

    = 154 sin ⁡ α 8 77 cos ⁡ α - 1 2 g 8 77 cos ⁡ α 2

    = 16 tan ⁡ α - 32   g 5929   cos 2   α

    Agora

    1 cos 2   α = sec 2   α = 1 + tan 2   α

    Então

    y frente = 16 tan ⁡ α - 32   g 5929 1 + tan 2   α

    ou

    tan 2   α - 5929 2   g tan ⁡ α + 1 + 5929 32   g y frente = 0

    Então

    tan ⁡ α = 5929 2   g ± - 5929 2   g 2 - 4 1 + 5929 32   g y frente 1 / 2 2

    ou

    tan ⁡ α = 5929 4 × 32.2 ± 5929 4 × 32.2 2 - 1 + 5929 32 × 32.2 y frente

    ou

    tan ⁡ α = 46.0326 ± 46.0326 2 - 1 + 5.7541   y frente 1 / 2

    Agora, 0 ≤ y frente ≤ 4   ft de modo que a raiz positiva produza valores de α > 45 ° para todos os valores de yfrente. Quando a raiz negativa é selecionada, α aumenta à medida que yfrente aumenta. Portanto, para α max , defina

    y frente = y C = 4   ft

    Então

    tan ⁡ α = 46.0326 - 46.0326 2 - 1 + 5.7541 + 4 1 / 2

    ou

    α max = 14.6604 °

    Passo 3

  2. Nós encontramos

t enter = 8 77 cos ⁡ α

= 8 77 cos ⁡ 14.6604 °

Resposta

a)   α max = 14.66 °

b)   t enter = 0.1074   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição de uma partícula é dada por s = 2 t 3 - 40 t 2 + 200 t - 50 , onde s é em metros e t é em segundos. Represente graficamente a posição, velocidade e aceleração como funções do tempo para os p
O deslocamento de uma partícula que se move ao longo do eixo s é dado por s = - 2 + 3 t e - 0,5 t , onde s é em metros e t é em segundos. Represente graficamente o deslocamento, a velocidade e a acele
A aceleração de uma partícula que está se movendo ao longo de uma linha reta a = - k v , onde a é em metros por segundo ao qudrado, k é uma constante, e v é a velocidade em metros por segundo. Determi
O piloto de um avião de transporte a jato leva os motores a plena potência de decolagem antes de liberar os freios enquanto a aeronave está parada sobre a pista. O empuxo do jato permanece constante,
Um avião a jato com uma velocidade de pouso de 200k m / h tem um máximo de 600m de pista disponível após tocar o solo no qual deve reduzir sua velocidade para 30k m / h . Calcule a aceleração média a