Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 16
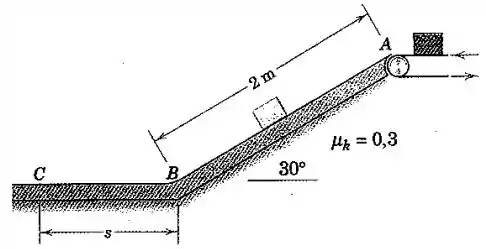
Um pequeno pacote é depositado pela correia transportadora em uma rampa com em com uma velocidade de . Calcule a distância sobre a superfície plana na qual o pacote atinge o repouso. O coeficiente de atrito dinâmico para o pacote e a superfície de suporte desde até é .
Passo 1
Na direção de descida do pacote, de até , atuam duas forças opostas: a componente do peso para baixo e a força de atrito para cima. Temos:
onde é a força normal, que anula a outra componente do peso :
Logo,
Passo 2
Para o trajeto de até , calculamos a aceleração através da aplicação da Segunda Lei de Newton:
E assim, podemos calcular a velocidade com a qual o pacote chega a , através da equação:
Passo 3
Beleza! De modo análogo, para o trajeto de até , podemos calcular a aceleração através da aplicação da Segunda Lei de Newton, mas agora a única força atuando será a força de atrito dinâmico , dada por:
Cuidado! A força normal aqui não será igual àquela força do trajeto de até ! Isso acontece porque lá a normal estava se equilibrando com apenas uma componente do peso, devido à inclinação. Porém, aqui a normal equilibra todo o peso, e portanto:
Agora sim, aplicamos a Segunda Lei de Newton:
Passo 4
Sabendo a velocidade inicial do trajeto e a aceleração constante , podemos, enfim, calcular a distância , através da equação: