Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 113

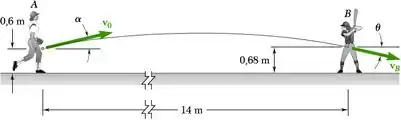
A lançadora de um jogo de softball arremessa uma bola com uma velocidade inicial v0 de 72 km/h a um ângulo α com a horizontal. Se a altura da bola no ponto B é de 0,68 m, determine (a) o ângulo α , (b) o ângulo θ que a velocidade da bola forma com a horizontal no ponto B.

Passo 1

E ai galera tudo certo? O enunciado pede que a gente encontre o ângulo α , o ângulo θ que a velocidade da bola forma com a horizontal no ponto B.

Primeira nota

v 0 = 72   km/h = 20   m/s

v x 0 = v 0 cos ⁡ α = 20   m/s cos ⁡ α

v y 0 = v 0 sin ⁡ α = 20   m/s sin ⁡ α

Passo 2

  1. Movimento horizontal. (Uniforme)

    2. x = 0 + v x 0 t = 20 cos ⁡ α t

    No Ponto B:

    14 = 20 cos ⁡ α t             o u             t B = 7 10 cos ⁡ α

    Movimento vertical. (Movimento uniformemente acelerado)

    y = 0 + v y 0 t - 1 2 g t 2 = 20 sin ⁡ α t - 1 2 g t 2               g = 9.81   m/ s 2

    No Ponto B:

    0.08 = 20 sin ⁡ α t B - 1 2 g t B 2

    Substituindo tB

    0.08 = 20 sin ⁡ α 7 10 cos ⁡ α - 1 2 g 2 7 10 cos ⁡ α 2

    8 = 1400 tan ⁡ α - 1 2 g 49 cos 2   α

    Agora

    1 cos 2   α = sec 2   α = 1 + tan 2   α

    Então

    8 = 1400 tan ⁡ α - 24.5 g 1 + tan 2   α

    ou

    240.345   tan 2   α - 1400 tan ⁡ α + 248.345 = 0

    Resolvendo

    α = 10.3786 °             e             α = 79.949 °

    Passo 3

  2. Nós temos

v x = v x 0 = 20 cos ⁡ α

e

v y = v y 0 - g t = 20 sin ⁡ α - g t

No Ponto B:

v y B = 20 sin ⁡ α - g t B

= 20 sin ⁡ α - 7 g 10 cos ⁡ α

Passo 3

Observando que no Ponto B, vy

tan ⁡ θ = v y B v x = 7 g 10 cos ⁡ α - 20 sin ⁡ α 20 cos ⁡ α = 7 200 9.81 cos ⁡ 10.3786 ° - sin ⁡ 10.3786 ° cos ⁡ 10.3786 °

Resposta

a)   R e j e i t a n d o   a   s e g u n d a   r a i z   p o r q u e   n ã o   é   f i s i c a m e n t e   r a z o á v e l ,   t e m o s   α = 10.38 °

b)   θ = 9.74 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A aceleração de uma partícula é dada por a ( t ) = 2 t - 10 , onde a é em metros por segundo ao quadrado e t é em segundos. Determine a velocidade e o deslocamento como funções do tempo. O deselocamen
A velocidade de uma partícula que se desloca ao longo do eixo s é dada por v = 2 - 4 t + 5 t 3 / 2 , onde t é em segundos e v é em metros por segundo. Calcule a posição s , a velocidade v , e a aceler
Uma bola é lançada verticalmente para cima com uma velocidade de 30m / s na borda de um penhasco com 60m . Calcule a altura h para a qual a bola se eleva e o tempo total t após a liberação para a bola
A aceleração de uma partícula é dada por a = - k s 2 , onde a é em metros por segundo ao quadrado, k é uma constante, e s é em metros. Determine a velocidade da partícula como uma função de sua posiçã
Dados experimentais para o movimento de uma partícula ao longo de uma linha reta forneceram medidas dos valores da velocidade v para várias coordenadas de posição s . Uma curva suave é desenhada passa