Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 12
Determine a tração na corda e as componentes horizontal e vertical da reação no apoio A da viga do problema 4
Passo 1
Falaa!
Vamos relembrar o problema 5.4:
Tínhamos essa viga, suportando um saco de 80 kg. Esse aí é o nosso diagrama de forças.
Ele quer que a gente descubra e , as reações em .
Percebe que temos uma polia ali. A corda que causa e é a mesma, logo as duas extremidades tem a mesma tensão, por isso a gente pode dizer que
E ele também nos pediu para descobrir , bora lá!
Passo 2
Como o peso da viga não nos foi dado vamos então vamos ignora-lo.
Como estamos trabalhando com sistema estáticos então Todas as Forças em x se anulam
Assim como Todas as Forças em y e o momento.
Podemos expressar dessa forma
Passo 3
Agora que já fizemos a parte mais difícil, que é pensar: Como eu resolvo esse pepino?! Só nos resta calcular. Rs
Vamos por partes. Começando por Fy.
Para achar esse , a figura do problema já nos da a dica, pois mostra um triangulo de base 3, altura 4 e hipotenusa 5.
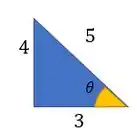
Aí temos que:
Logo nossa equação fica
Passo 4
Esse já é um bom início. Vamos usar agora o momento para dar o xeque mate.
O segredo é calcular o momento em relação ao ponto onde temos mais forças desconhecidas. Vamos calcular o somatório dos momentos em relação ao ponto . Ele vai ser dado pela soma dos termos:
Onde é a distância de até o ponto de aplicação da força usada.
A projeção de sobre o eixo não vai causar momento em , porque sua linha de ação passa por , portanto apenas a projeção de sobre o eixo irá causar momento em , e essa projeção é dada por: .
Se a gente considerar o momento no sentido anti-horário positivo, temos algo assim:
Isolando :
Substituindo isso em :
Isolando
Isso indica que essa força na verdade está para baixo.
Passo 5
Para finalizar:
Pelo triângulo retângulo
Então