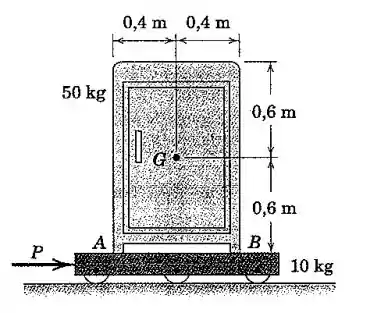
Determine o valor da força P que faria o armário começar a se inclinar. Qual coeficiente de atrito estático é necessário para assegurar que a inclinação ocorra sem deslizamento?

Pessoal, a primeira coisa que devemos fazer é desenhar o diagrama de corpo livre. Ao olharmos o conjunto como um todo, temos as seguintes forças atuando:

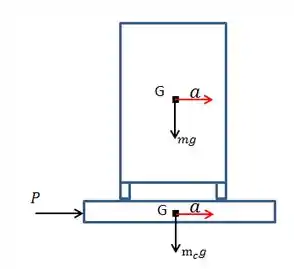
Então, pela equação de equilíbrio de forças no eixo x, temos:

Agora, vamos fazer um diagrama de corpo livre apenas para o armário. Teremos as seguintes forças atuando:

No instante que o armário começa a inclinar, não há força atuando em B, pois não há mais contato. Já no ponto A, temos atuando a normal e a força de atrito que é responsável pela aceleração do armário.

Podemos calcular a aceleração a partir o somatório dos momentos no ponto A:

Pelas equações de equilíbrio em x e y, temos que:

Dividindo estas duas equações, encontramos que:

É o valor mínimo para não haver deslizamento. Portanto:

Agora para encontrar a força P, basta substituirmos a equação (2) na (1):