Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 203

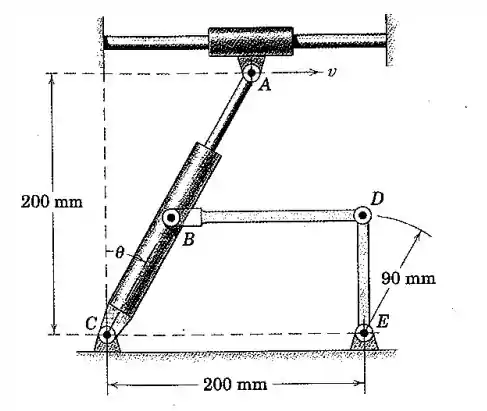
Para a posição mostrada onde θ = 30 ° , o ponto A sobre o cursor deslizante possui uma velocidade constante v = 0,3   m / s com o correspondente aumento do cilindro hidráulico AC. Para essa mesma posição BD é horizontal e DE é vertical. Determine a aceleração angular α D E de DE nesse instante.

Passo 1

Bom pessoal, como é de costume, vamos fazer um esboço do mecanismo com os vetores velocidade. Lembrando que o cursor se move na direção horizontal para a direita. E também que velocidades de pontos que pertencem a hastes rígidas, como B e D, possuem direção perpendicular às mesmas (no caso AC e DE, respectivamente).

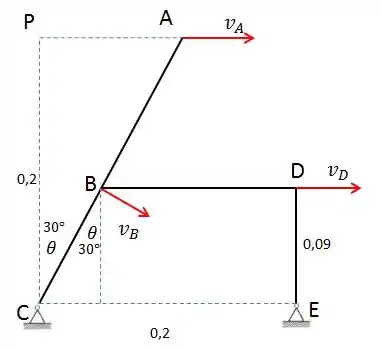
Algumas relações geométricas podem ser tiradas da figura:

B C = 0,09 c o s 30 = 0,104   m

D B = 0,2 - 0,09 t a n 30 = 0,148   m

Neste caso, temos que A percorre sempre a trajetória horizontal, pois o cilindro permite que AC aumente de tamanho para atender. Portanto, podemos escrever o vetor posição de A através de uma relação geométrica:

x A = 0,2 t a n θ

Com isso, podemos calcular sua velocidade e aceleração através de suas derivadas em função do tempo. OBS Lembre-se sempre da regra da cadeia:

v A = x ˙ A = 0,2 θ ˙ sec 2 ⁡ θ

a A = x ¨ A = 0,2 θ ¨ sec 2 ⁡ θ + 0,2 2 θ ˙ 2 s e c θ ( s e c θ t a n θ )

Agora, como neste instante θ = 30 ° , v A = 0,3 m s   e   a A = 0   m / s 2 , podemos calcular os valores das variáveis acima:

x A = 0,1155   m

v A = 0,3 m s = 0,2 θ ˙ sec 2 ⁡ θ

θ ˙ = 1,125   r a d / s

a A = 0 = 0,2 θ ¨ sec 2 ⁡ θ + 0,2 2 θ ˙ 2 s e c θ ( s e c θ t a n θ )

θ ¨ = - 1,461 r a d s 2 = 1,461 k ^ r a d s 2 e m   n o t a ç ã o   v e t o r i a l

Pronto! Esta parte era a mais importante e mais difícil da questão.

Agora, sabendo a velocidade angular do cilindro AC, θ ˙ , podemos calcular a velocidade de B:

v B = θ ˙ × B C = 1,125 × 0,104 = 0,117   m / s

A velocidade de D pode ser também calculada a partir do diagrama dos vetores velocidade v B ,   v D   e   v D / B . Vamos ver:

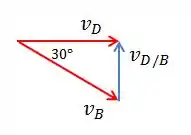
Temos então que:

v D = v B c o s 30 = 0,1013   m / s

v D B = v B s e n 30 = 0,0585   m / s

Passo 2

Agora vamos para as acelerações.

A aceleração de B pode ser calculada a partir do cilindro AC:

a B = a B n + a B t

Onde:

a B n = - r B C θ ˙ 2 = - 0,09 t a n 30   i ^ + 1 j ^ 1,125 2 = - 0,0678   i ^ - 0,114 j ^   m / s 2

a B t = θ ¨ × r B C = 1,461 k ^ × 0,09 t a n 30   i ^ + 1 j ^ = 0,0759 j ^ - 0,1315 i ^   m / s 2

E ainda, a aceleração de D pode ser calculada a partir da haste DE:

a D = a D n + a D t

Onde:

a D n = - r D E ω 2 = - r D E v D r D E 2 = - j ^ 0,1013 2 0,09 = - 0,114 j ^   m / s 2

a D t = α D E × r D E = α D E k ^ × 0,09 1 j ^ = - 0,09 α D E i ^   m / s 2

Bom, a aceleração relativa entre os pontos D e B pode ser escrita pela equação:

a D = a B + a D / B n + a D / B t

Da mesma forma que foi feita aí em cima, vamos calcular a D / B n e   a D / B t :

a D / B n = - r D B ω D B 2 = - r D B v D B r D B 2 = - 0,0585 2 0,148 i ^ = - 0,0231 i ^   m / s 2

a D / B t = α D B × r D B = 0,118 α D B j ^   m / s 2

Agora, vamos substituir todos os valores calculados na equação da aceleração relativa:

- 0,114 j ^ - 0,09 α D E i ^ = - 0,0678   i ^ - 0,114 j ^ + 0,0759 j ^ - 0,1315 i ^ - 0,0231 i ^ + 0,118 α D B j ^

Decompondo nas direções:

- 0,09 α D E i ^ = - 0,0678   i ^ - 0,1315 i ^ - 0,0231 i ^

- 0,114 j ^ = - 0,114 j ^ + 0,0759 j ^ + 0,118 α D B j ^

Resolvendo o sistema:

α D E = 2,45 k ^   r a d / s 2

α D B = - 0,64 k ^   r a d / s 2

Resposta

α D E = 2,45 k ^   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco gira em torno do eixo z w z = 0,5r a d / s sem deslizar no plano horizontal. Se nesse mesmo instante w z está aumentando a ω ˙ z = 0,3r a d / s 2 , determine a velocidade e a aceleração do pon
A lança do guindaste AO gira em torno dp eixo z com uma velocidade angular constante w 1=0,15r a d / s , enquanto ela está girando para baixo com uma velocidade angular constante w 2=0,2r a d / s . De
No instante mostrado, o guindaste da torre gira em torno do eixo z com uma velocidade angular ω 1 = 0,25r a d / s , a qual está aumentando a 0,6r a d / s ² ². A lança do guindaste AO gira para baixo c
Se a engrenagem de cima B gira a uma taxa constante ω , determine a velocidade angular da engrenagem A, que está livre para girar em torno do eixo e rola sobre a engrenagem fixa de baixo C.
O telescópio está montado sobre uma estrutura F que permite ser direcionado para qualquer ponto do céu. No instante θ = 30 ° , a estrutura tem uma aceleraçãoαy = 0,2r a d / s 2 e uma velocidade angula