Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 226
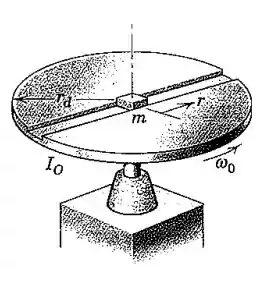
O pequeno bloco de massa m desliza na ranhura radial lisa do disco, que gira livremente em seu mancal. Se o bloco é ligeiramente deslocado da posição central quando a velocidade angular do disco é , determine sua velocidade radial como uma função da distância radial r. O momento de inércia de massa do disco em relação ao seu eixo de rotação é
Passo 1
Pessoal, vamos representar o disco e o bloco pela vista superior.
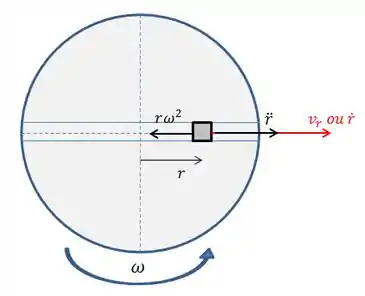
A aceleração resultante na direção radial r é igual a diferença entre a aceleração linear do bloco e da aceleração normal devido à rotação do sistema.
Neste instante, a velocidade angular do sistema não é a mesma da condição inicial, devido ao deslocamento do bloco de massa m. Para encontrar o , devemos usar a conservação de momento angular (lembrando-se de usar o teorema dos eixos paralelos para o bloco):
Beleza! Agora, vamos usar a equação de equilíbrio das forças na direção radial para o bloco.
Como não há nenhuma força externa atuando no bloco:
Substituindo o valor de
Passo 2
Agora vem o grande pulo do gato desta questão. O enunciado pede a velocidade radial e nós temos somente a aceleração. Porém, existe uma relação importante:
Esta relação vem da regra da cadeia. Vamos lá! A derivada da velocidade em função da posição pode ser escrita como:
A função é inversível, pois só há um valor de r para cada t. Vale então a relação:
E ainda temos que:
Substituindo na equação anterior:
E enfim chegamos a:
Passo 3
Agora sim!!! Voltando ao problema.
Multiplicando os dois lados por
E Integrando:
E tem mais algebrismo vindo ai.
Vamos fazer uma substituição de variável:
Voltando pra integral:
Agora dá pra resolver de boa:
Voltando para a variável
Aplicando as condições de contorno:
Finalmente, podemos substituir na equação (1):
Pra deixar igual a resposta do livro: