Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 25

Encontre os componentes do vetor de aceleração a em coordenadas esféricas.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.

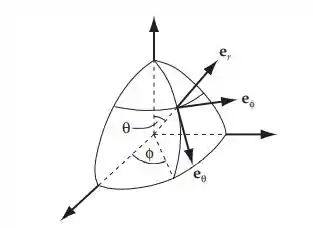
Os vetores unitários em coordenadas esféricas são expressos em termos de coordenadas retangulares por:

e θ = cos ⁡ θ cos ⁡ ϕ , cos ⁡ θ s e n   ϕ ,   - s e n   ϕ ,   e ϕ = - s e n   ϕ , cos ⁡ ϕ ,   0   e   e r = s e n   θ cos ⁡ ϕ ,   s e n   θ s e n   ϕ , cos ⁡ θ

Daí, temos que:

e ˙ θ = - ϕ ˙ cos ⁡ θ s e n   ϕ - θ ˙ s e n θ cos ⁡ ϕ , ϕ ˙ cos ⁡ θ cos ⁡ ϕ - θ ˙ s e n   θ s e n   ϕ ,   - θ ˙ cos ⁡ θ = - θ ˙ e r + ϕ ˙ cos ⁡ θ e ϕ

De forma similar temos que:

e ˙ ϕ = - - ϕ ˙ cos ⁡ ϕ ,   - ϕ ˙ s e n   ϕ , 0 = - ϕ ˙ cos ⁡ θ e θ - ϕ ˙ s e n   θ e r

e ˙ r = ϕ ˙ s e n   θ e ϕ + θ ˙ e θ

Agora, seja qualquer vetor posição x. Então:

x = r e r = > x ˙ = r e ˙ r + r ˙ e r = r ϕ ˙ s e n   θ e ϕ + θ ˙ e θ + r ˙ e r = r ϕ ˙ s e n   θ e ϕ + r θ ˙ e θ + r ˙ e r

= > x ¨ = r ˙ ϕ ˙ s e n   θ + r θ ˙ ϕ ˙ cos ⁡ θ + r ϕ ¨ s e n   θ e ϕ + r ϕ ˙ s e n   θ e ˙ ϕ + r ˙ θ ˙ + r θ ¨ e θ + r θ ˙ e ˙ θ + r ¨ e r

+ r ˙ e ˙ r = 2 r ˙ θ ˙ s e n   θ + 2 r θ ˙ ϕ ˙ cos ⁡ θ + r ϕ ¨ s e n   θ e ϕ + r ¨ - r ϕ ˙ 2 s e n 2 θ - r θ ˙ 2 e r

+ 2 r ˙ θ ˙ + r θ ¨ - r ϕ ˙ 2 s e n θ cos ⁡ θ e θ

Simplificando, temos que:

x ¨ = a = r ¨ - r ϕ ˙ 2 s e n 2 θ - r θ ˙ 2 e r + 1 r d d t r 2 θ ˙ - r ϕ ˙ 2 s e n θ cos ⁡ θ e θ

+ 1 r s e n   θ d d t r 2 ϕ ˙ s e n 2 θ e ϕ

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Uma força é especificada pelo vetor F = 120 i - 160 j + 80kN . Calcule os ângulos entre F e os eixos positivos x , y e z .
Determine a intensidade da força F de modo que a força resultante F R das três forças seja a menorpossível. Qual é a intensidade mínima de F R ?Fonte: Estática Mecânica para Engenharia – 14ª ed
Determine o erro percentual n ao substituir-se o seno e tangente de um ângulo pelos valores do ângulo em radianos de 5 ° , 10 ° e 20 ° . Explique a diferença qualitativa entre os resultados de seno e
Para os vetores V 1 e V 2 do Prob. ½, determine o módulo da diferença vetorial V ' = V 2 - V 1 e o ângulo θ x que V ' faz com o eixo positivo x . Complete tanto a solução gráfica quanto a algébrica.