Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 126

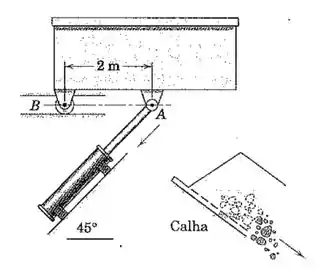
Um recipiente para resíduos é descarregado pelo mecanismo ativado hidraulicamente. Se a haste do pistão parte do repouso na posição indicada e possui uma aceleração de 0,5 m/s² no sentido mostrado, calcule a aceleração angular inicial do recipiente.

Passo 1

De acordo com o mecanismo, podemos ver que o ponto B se desloca na horizontal e o ponto A acompanha a descida do pistão a 45 ° .

Para calcular a aceleração angular do recipiente, usaremos a equação da aceleração relativa nos pontos A e B:

a A = a B + ( a A / B ) n + ( a A / B ) t

Onde:

( a A / B ) n = ω × ( ω × r ) → é a aceleração relativa normal e ela aponta para dentro de AB.

( a A / B ) t = α × r → é a aceleração relativa tangencial e ela é perpendicular à distancia AB.

Ah, um dado muito importante: Como o mecanismo parte do repouso, então sua velocidade angular ω   inicial é nula e consequentemente também sua aceleração normal   ( a A / B )   n = 0 .

Passo 2

Após a análise do problema, podemos esboçar o mecanismo com seus vetores aceleração.

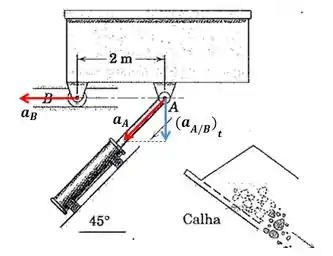
Usando apenas os vetores, temos:

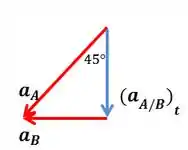
Sabemos que a A = 0,5   m / s 2 , então:

a A   c o s 45 ° = ( a A / B ) t   = α × r  

- 0,5 2 2 = α × 2

α = - 0,177   k ^   r a d / s 2

Resposta

α = - 0,177   k ^   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem está parado na plataforma em O e corre para fora na dreção da beira da plataforma de tal maneira que, quando eles está em A, y=1,5m, seu centro de massa tem uma velocidade de 0,6 m/s e uma ac
O raio do pino B fixo à manivela AB desliza livremente ao longo da ranhura no membro CDE. Se AB gira com o movimento mostrado, determine a velocidade angular de CDE no instante mostrado.
A lança telescópica do guindaste gira com a velocidade angular e a aceleração angular mostradas. No mesmo instante, a lança está se estendendo com uma velocidade constante de 0,15 m/s, medida em relaç
No instante θ = 45 ° , o membro DC tem uma velocidade angular ω D C = 4r a d / s e uma aceleração angular α D C = 2r a d / s 2 . Determine a velocidade angular e a aceleração angular da barra AB nesse
No instante mostrado, a barra AB tem uma velocidade angular ω A B = 4r a d / s e uma aceleração angular α A B = 2r a d / s 2 . Determine a velocidade angular e a aceleração angular da barra CD nesse i