Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 127
A viga de aço de 9m está sendo levantada a partir de sua posição horizontal pelos dois cabos presos em A e B. Se as acelerações angulares iniciais dos tambores de elevação são e nos sentidos indicados, determine a aceleração angular correspondente da viga, a aceleração de C, e a distância b desde B até um ponto P sobre a linha de centro da viga que não possui aceleração.
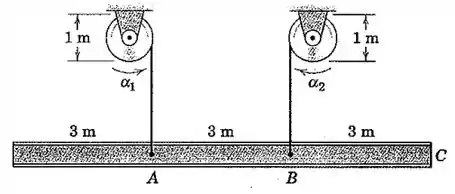
Passo 1
Neste exercício existem dois tambores com duas acelerações angulares diferentes. Além disso, são pedidos para encontrar 3 dados, ou seja, são 3 exercícios em 1.
Portanto, é importante definir muito bem as etapas e ordem de desenvolvimento.
Primeiramente, vamos calcular as acelerações dos pontos A e B:
Para calcular a aceleração angular da viga, usaremos a equação da aceleração relativa nos pontos A e B:
Onde:
é a aceleração relativa normal e ela aponta para dentro de AB.
é a aceleração relativa tangencial e ela é perpendicular à distancia AB.
Importante: O sistema parte do repouso, pois o enunciado diz que a viga inicia o movimento na horizontal. Então sua velocidade angular inicial é nula e consequentemente também sua aceleração normal
Passo 2
O primeiro item a ser encontrado é a aceleração angular da viga. Como já sabemos a aceleração de 2 pontos dela, podemos aplicar a equação da aceleração angular:
Encontramos nossa primeira resposta.
Passo 3
Agora, podemos aplicar a mesma equação para encontrar a aceleração do ponto C.
Passo 4
Por fim, podemos calcular a distancia b por dois métodos diferentes:
- Por semelhança de triângulos ou;
- Pela equação da aceleração relativa.
Para ficar igual ao desenvolvimento dos itens acima, vamos fazer por aceleração relativa.
Mas vale a pena ver o diagrama abaixo para visualizar o problema como um todo.
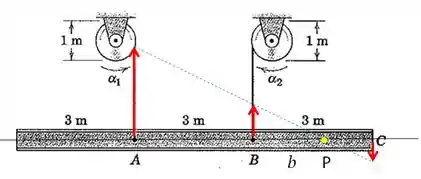
Vamos lá. Como não há aceleração em P: