Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 82

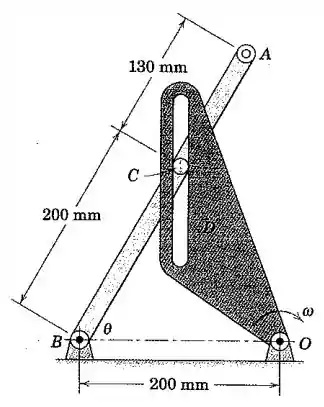
Para o instante representado, o elemento gira com uma velocidade angular e sua ranhura está vertical. Também nesse instante, . Determine a velocidade da extremidade da barra para esse instante.

Passo 1

Vamos considerar como um ponto do elemento , coincidindo com o pino da barra . Vetorialmente, podemos escrever:

Com base na figura, como e as distâncias e são iguais, os vetores dessas velocidades ficarão representados assim:

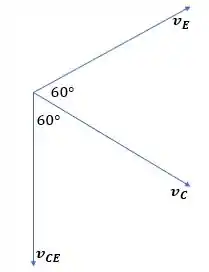
Sendo assim, temos .

Passo 2

Como é um ponto de , o módulo de sua velocidade é dado por:

onde . Porém, o ponto coincide com o ponto , então . Portanto, quando , e assim obteremos:

Como já vimos, temos , logo:

Passo 3

Com a velocidade do ponto , podemos descobrir a velocidade angular da barra :

onde :

Portanto, a velocidade de será dada por:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/110) A roda motriz traseira de um automóvel tem um diâmetro de 650m m e tem uma velocidade angular N de 200r p m em uma estrada coberta de gelo . Se o centro instantâneo de velocidade nula está 100m

5/94) A barra com restrições do Prob.5/81 é reapresentada aqui . A extremidade A da barra possui uma velocidade descendente v A de 2 m / s durante um intervalo de seu movimento . Para a posição onde θ

5/96) Para o instante representado , quando a manivela O A passa pela posição horizontal , determine a velocidade do centro G da barra A B pelo método dessa seção .

5/107) Ocorpo retangular B é articulado à manivela O A em A e é apoiado pela roda em D . Se O A possui uma velocidade angular no sentido anti-horário de 2r a d / s , determine a velocidade do ponto E

5/101) O mecanismo do Prob.5/27 é reapresentado aqui. No instante em que x A = 0,85 L , a velocidade do cursor em A é v = 2 m / s para a direita . Determine a velocidade correspondente do cursor B e a