Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 8
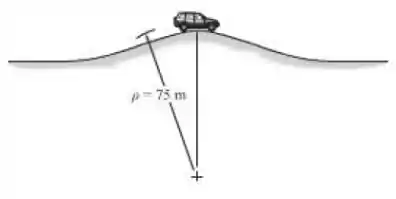
Determine a velocidade máxima que o jipe pode se mover sobre o cume do monte sem perder o contato com a estrada.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
A máxima velocidade sem que o carro perca o contato com a estrada será atingida no limite quando a força normal é nula! Esta relação será chave para resolvermos nosso problema!
Passo 2
Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, temos:
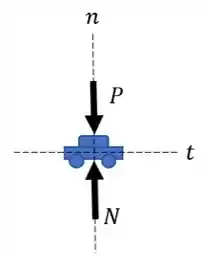
O nosso carro está sujeito apenas a presença das forças peso e normal. Entretanto, como dito no Passo 1, a força normal é nula!
Passo 3
Vamos descobrir a velocidade máxima que o carro pode passar pelo cume do monte. Sabendo que a força normal é zero e ele está sujeito a uma aceleração normal, pois está em uma trajetória curvilínea, temos:
Observem que o valor da aceleração foi colocado para baixo (negativa), na direção do centro da curvatura!