Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 223
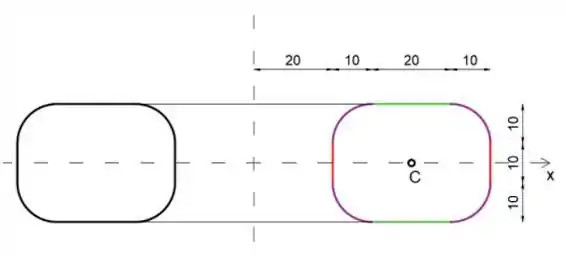
Determine o volume V e a área de superfície total A do anel completo que é mostrado na seção. Todos os quatro raios de canto da seção transversal são de 10 mm.
Passo 1
Usando o teorema de Pappus, podemos escrever a expressão para a área como:
(1)
Onde x é o centróide das linhas, L é o comprimento das linhas e θ ângulo de rotação
Consideraremos toda a circunferência como uma linha de comprimento:
E uma vez que a linha é simétrica a: -eixo paralelo ao ponto C, seu centróide está no ponto C, ou seja, a distância entre o centróide e o eixo-z é:
O ângulo de rotação é
Coloque os valores na expressão (1)
Passo 2
Usando o teorema de Pappus, podemos escrever a expressão para a área como:
(2)
Onde x ‾ é o centroide da área, A é a área e o ângulo de rotação θ
Observe que a área total de uma seção transversal é:
Com o centróide no ponto Cs
E o ângulo de rotação
Coloque todos os valores na expressão (2)
O volume total
