Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 91
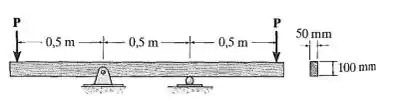
A viga tem a seção transversal retangular mostrada na figura. Se P = 1,5 kN, determine a tensão de flexão máxima na viga. Faça um rascunho da distribuição de tensão que age na seção transversal.
.
Passo 1
Falaa galerinha bonita, tudo beleza?!
Saca só, nesse exercício aqui o enunciado nos diz que a viga tem a seção transversal retangular como mostrado na figura. Sabendo que , o enunciado nos pede para determinar a tensão de flexão máxima na viga.
Iradoso, pra gente achar esse valor, precisamos achar a expressão para a tensão máxima do momento. Então podemos usar essa fórmulinha:
Logo, se a gente encontrar os valores da coordenada , do momento de inércia e do momento fletor , vamos conseguir resolver a questão. Bora lá!
Passo 2
Belezoca, como vimos na fórmula, é o momento de inércia da nossa seção em relação ao eixo . Ele vai ser dado por
Enquanto que é a maior distância entre e a borda da seção, no caso:
Passo 3
Falta , que é o momento máximo na viga.
Precisamos então ver onde o momento nessa viga é máximo. Podemos ver isso pelo diagrama de momento fletor.
Por simetria, as cargas nos dois apoios também valem . Mas como queremos o momento fletor máximo, podemos usar da malandragem e fazer o cálculo das cargas , tal que:
Logo:
Portanto, o momento máximo será:
Passo 4
Agora vamos montar nossa tensão máxima:
Passo 5
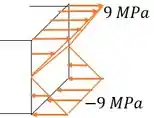
Só falta fazer um esboço da seção que tem essa seção máxima, para mostrar a distribuição de tensão na seção.
Como fica? A gente tem que nas bordas, em , a tensão é máxima, e vale . Mas devido a orientação do momento, na parte de baixo temos compressão, logo as setinhas estarão para dentro, e na parte de cima temos tração (setinhas para fora).
Temos também que vai ser o eixo neutro da nossa seção, ou seja, onde . Sendo assim, a distribuição de tensão no sentido vertical da seção é linear, e no sentido horizontal, é constante. O esboço fica assim:
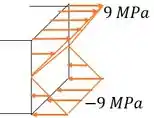
Resposta
