Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 80
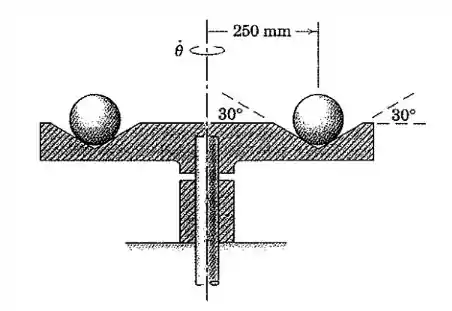
O disco com a caneleta circular gira em torno do eixo vertical com uma rotação constante de e suporta duas esferas de . Calcule a maior das duas forças de contato entre o disco e cada esfera. (Este resultado pode ser obtido usando apenas uma equação de força?)
Passo 1
Primeiro precisamos entender o seguinte: existem duas forças de contato agindo sobre cada esfera, uma para cada “lado” da vala onde as esferas estão presas. Vamos dar nome a essas forças:
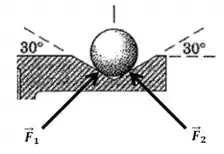
E o que a gente tem que exigir dessas forças para que o sistema esteja em equilíbrio? Na vertical elas precisam anular a força peso, e na horizontal elas precisam fazer o papel de força centrífuga.
As componentes verticais dessas duas forças são:
E as horizontais são:
Passo 2
E agora vamos impor as condições que mencionamos ali em cima. As forças verticais tem que compensar o peso:
E as forças horizontais tem que fazer o papel da força centrípeta:
Pronto, agora ficamos com um sistema de duas variáveis e duas equações, é só resolver!
Passo 3
O sistema é:
E então:
Somando as duas equações:
E subtraindo a primeira da segunda:
Ou seja, a maior das duas forças de contato é .
Passo 4
Será que podemos obter esse resultado usando apenas uma equação de força? Bom, nesse caso precisaríamos aplicar a segunda lei de Newton de forma que apenas a força (que é quem queremos calcular) aparecesse.
Podemos conseguir isso se aplicarmos a segunda lei em uma direção perpendicular à força ! Veja no desenho:
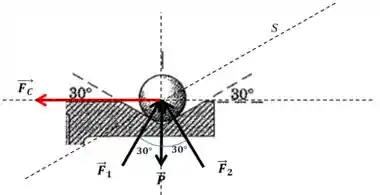
E como no fim das contas a única força resultante atuando sobre a esfera é a força centrípeta, podemos aplicar a lei de Newton naquela direção para achar a seguinte equação:
O que concorda com o nosso resultado anterior!
Resposta
A maior das duas forças de contato mede .