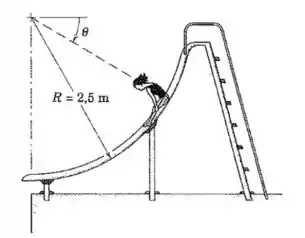
A partir do repouso em que , uma criança de desliza com atrito desprezível para baixo no escorrega que tem a forma de um arco circular com raio de . Determine a aceleração tangencial e a velocidade da criança, e a força normal exercida sobre ela (a) quando e (b) quando .
Passo 1
Vamos começar desenhando as forças envolvidas:
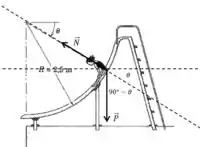
Nessa situação, é importante saber quem cumpre o papel de força tangencial e de força normal:
Passo 2
Olhando para essas equações fica fácil calcular a aceleração tangencial:
E ainda podemos usar a aceleração tangencial para calcular a velocidade:
Mas , então podemos reescrever:
E podemos integrar essa equação para achar uma fórmula geral para a velocidade em função do ângulo:
Passo 3
E agora fica fácil achar uma fórmula para a força normal também, já que:
E agora já temos todas as fórmulas de que precisamos.
Passo 4
(a) Quando , temos:
E quando
Resposta
(a) ; ; .
(b) ; ; .