Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 93
Um pequeno veículo entra no topo da trajetória circular com uma velocidade horizontal e ganha velocidade conforme se desloca pra baixo na trajetória. Determine uma expressão para o ângulo que localiza o ponto onde o veículo sai da trajetória e se torna um projétil. Avalie sua expressão para . Despreze o atrito e trate o veículo com uma partícula.
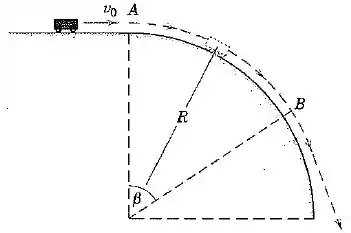
Passo 1
Na direção normal temos uma componente do peso e a força normal, e juntas elas precisam gerar uma resultante centrípeta:
E aqui estamos considerando que o sentido positivo aponta para o centro da trajetória.
Na direção tangencial temos apenas a outra componente do peso:
Quando o veículo perde contato com o chão a força normal é nula, então, pela primeira equação:
Beleza, já temos uma fórmula para o ângulo em que a perda de contato acontece, mas falta determinar a velocidade nesse ponto.
Passo 2
Para encontrar uma equação para a velocidade podemos usar a equação de Torricelli, mas de um jeito bastante incomum.
Essa equação exige que e estejam na mesma direção, certo? Então se considerarmos , isso quer dizer que estamos pensando na direção vertical e para baixo, e por isso também ter que ser o deslocamento medido nessa direção.
Vamos procurar uma fórmula para o deslocamento vertical do carro para um certo ângulo :
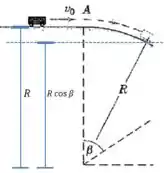
Olhando para essa figura temos:
E então a nossa equação fica:
Passo 3
Agora podemos substituir isso de volta na equação do passo :
Beleza, chegamos na expressão que queríamos, agora vamos calcular no caso em que :
Pronto!
Resposta
A expressão para o ângulo em que o veículo sai da trajetória é e para .