O caminhão-plataforma parte do repouso em uma estrada cujo raio de curvatura constante é e cujo ângulo de inclinação lateral é . Se a aceleração constante do caminhão para frente é , determine o tempo após o início do movimento no qual o caixote sobre a plataforma começa a deslizar. O coeficiente de atrito estático entre o caixote e a plataforma do caminhão é , e o movimento do caminhão ocorre em um plano horizontal.
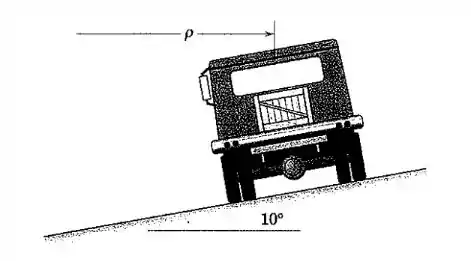
Passo 1
Vamos definir algumas direções nessa situação:
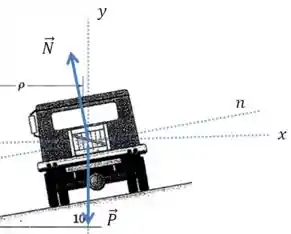
E essas forças precisam estar equilibradas por uma força de atrito que vai estar no plano da carroceria do caminhão.
Vamos considerar então que ela tem duas componentes: uma na direção da reta pontilhada , e uma na direção do movimento do caminhão, perpendicular ao plano da página.
Passo 2
Então vamos escrever as condições para que o sistema fique em equilíbrio.
Na direção da reta , a soma das forças é:
Na direção da reta tem que haver uma resultante centrípeta, então:
Mas como e , sabemos que , então:
E na direção perpendicular ao plano da página temos apenas o movimento do caminhão
Então ficamos com o seguinte sistema:
Passo 3
Podemos usar as duas primeiras equações para calcular os valores de e :
Precisamos multiplicar a equação de cima por , e a de baixo por , e então subtrair a primeira da segunda:
E então:
E fazendo o contrário para achar a normal:
Com isso já temos as fórmulas para , e .
Passo 4
Conforme falamos antes, as forças e são as duas componentes da força de atrito, ou seja:
Mas pela definição da força de atrito:
Podemos dividir tudo pela massa:
E agora precisamos resolver para encontrar o valor de .
Passo 5
Vamos começar abrindo os parênteses:
E agora vamos substituir os valores numéricos:
E agora podemos fazer uma substituição simples:
E resolver como se fosse uma equação quadrática:
E descartando a solução negativa:
E esse é o instante de tempo em que o bloco começa a deslizar!
Resposta
O instante em que começa a haver deslizamento é .