Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 241
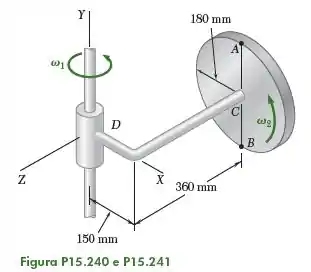
Um disco com raio de gira à taxa constante em relação ao braço , que por sua vez gira à taxa constante em torno do eixo . Determine, no instante mostrado na figura, a velocidade e a aceleração do ponto na periferia do disco.
Passo 1
Oi pessoal... O exercício nos pede para determinar a velocidade e a aceleração do ponto quando e .
A velocidade escalar do ponto será:
Sabendo que:
E:
Vamos aos cálculos.
Passo 2
Temos os seguintes vetores posições:
E:
Portanto:
E:
Logo, a velocidade escalar do ponto será:
Passo 3
Para a aceleração do ponto , temos que:
Temos que:
Portanto:
Temos também que:
Portanto:
Resposta
Exercícios de Livros Relacionados
O colar P desliza para fora a uma velocidade relativa constante u ao longo da barra AB, que gira no sentido anti-horário com uma velocidade angular constante de 20r p m . Sabendo que r = 250m m quando
O pino P desliza em uma ranhura circular cortada na placa mostrada na figura com uma velocidade relativa constante u = 90m m / s . Sabendo que, no instante mostrado, a velocidade angular ω da placa é
Sabendo que, no instante mostrado na figura, a barra articulada em B gira no sentido anti-horário com velocidade angular constante ω B de 6 rad /s, determine a velocidade angular e a aceleração angula
O pino P desliza em uma ranhura circular cortada na placa mostrada na figura com uma velocidade relativa constante u = 90m m / s . Sabendo que, no instante mostrado, a velocidade angular ω da placa é
No instante mostrado na figura, a barra BC tem uma velocidade angular de 3r a d / s e uma aceleração de 2r a d / s 2 , ambas no sentido horário. Determine a aceleração angular da placa.