Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 10

Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do semielipsoide.

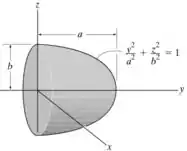
Passo 1

Sabemos que d m = ρ d V e, para o cone em questão, podemos considerar o elemento diferenciável d V como sendo π r 2 d y . O raio seria uma parte do eixo z que quando o calculamos por semelhança de triângulo, vamos chegar na igualdade r = z = b 1 - y 2 a 2 . Então, podemos escrever,

d m = ρ π b 1 - y 2 a 2 2 d z

A fórmula acima é a parte diferenciável. Para encontrarmos o massa, vamos integrar a parte diferenciável de 0 a a . Então,

m = ∫ d m = ∫ o a ρ π b 1 - y 2 a 2 2 d y = 2 3 ρ π a b 2

Passo 2

O momento de inércia do elemento pode ser calculado por:

d I y = 1 2 r 2 d m = 1 2 r 2 ρ π r 2 d y = 1 2 ρ π r 4 d y = 1 2 ρ π b 1 - y 2 a 2 4 d y

A fórmula acima é a parte diferenciável. Para encontrarmos o momento de inércia, vamos integrar a parte diferenciável de 0 a a . Então,

I y = ∫ d I y = ∫ o a 1 2 ρ π b 1 - y 2 a 2 4 d y = 4 15 ρ π a b 4

Passo 3

Encotramos o valor da massa e do mometo de inércia. Agora basta fazermos um uma jogada matemática para colocar a massa dentro do momento de inércia. Então,

I y = 4 15 ρ π a b 4 = 2 3 ρ π a b 2 2 5 b 2 = 2 5 m b 2

Resposta

I y = 2 5 m b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, a barra fina uniforme de 30 kg tem uma velocidade angular no sentido horário de ω = 6r a d / s . Determine as componentes normais e tangenciais da reação do pino O sobre a barra
A barra uniforme tem uma massa de 15 kg. Determine as componentes verticais e horizontais da reação no pino O, e a aceleração angular da barra logo após a barra ser cortada.
O hemisfério é formado girando-se a área sombreada em torno do eixo y . Determine o mometo de inércia I y e expresse o resultado em termos da massa total m do hemisfério. O material tem uma densidade
Determine o momento de inércia I y para a barra fina. A densidade da barra ρ e a área de seção transversal A são constante. Expresse o resultado em termos da massa total m da barra.
Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo centro de massa G . O material tem um peso específico de γ = 15KN/m3.