Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 23
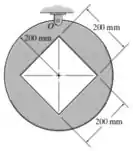
Determine o momento de inércia da massa da placa fina em relação a um eixo perpendicular à página e passando pelo ponto . O material tem uma massa por unidade de área de 20 kg/m2.
Passo 1
O círculo pode ser subdivido em duas partes, sendo elas: a placa quadrada e o círculo sem o quadrado no centro. Podemos calcular as massas de cada uma dessas partes, com isso,
e
Passo 2
A partir do cálculo das massas, podemos calcular o momento de inércia passando pelo ponto através do teorema dos eixos paralelos. Então,
Resposta
Exercícios de Livros Relacionados
Determine o momento de inércia da massa da placa fina em relação a um eixo perpendicular à página e passando pelo ponto O . O material tem uma massa por unidade de área de 20kg/m2.
O recipiente uniforme de 4 Mg contém lixo nuclear encapsulado em concreto. Se a massa da viga de sustentação BD é 50kg, determine a maior aceleração vertical a do sistema de maneira que cada um dos me
Quando o mecanismo de içamento está operando, a carga de 2000N é submetida a uma aceleração para cima de 1,5 m/s2. Determine a força compressiva que a carga cria em cada uma das colunas, AB e CD. Qual
Se o anel grande, o anel pequeno e cada um dos arcos têm uma massa de 50kg, 7,5kg e 10kg, respectivamente, determine o momento de inércia de massa da roda em relação a um eixo perpendicular à página e
Determine o momento de inércia da massa do pêndulo em relação a um eixo perpendicular à página e passando pelo ponto O . A barra fina tem uma massa de 10kg e a esfera tem uma massa de 15kg.