Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 20

Para o conjunto do Problema, determine (a) a quantidade de movimento angular em relação a B, (b) o ângulo formado entre a quantidade de movimento angular e o eixo BA.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente determine (a) a quantidade de movimento angular em relação a B, (b) o ângulo formado entre a quantidade de movimento angular e o eixo BA.

W = 4   l b ,               m = 4 32.2 = 0.12422   l b ∙ s 2 /   f t   ,                 a = 8   i n . = 0.66667   f t

ω = ( 2   π ) ( 240 ) 60 = 8   π   r a d / s ,           ω x = 0 ,           ω y = 0 ,           ω z = 8   π   r a d / s

Passo 2

Use eixos paralelos x ´ , y ´ , z , com origem no ponto A, como mostrado:

( H B ) x = - I x z ω

( H B ) y = - I y z ω

( H B ) z = - I z ω

Segmentos 1, 2, 3 e 4, cada um com massa m ´ = 0.06211   l b ∙ s / f t , contribu em I x z ,       I y z , para I z .

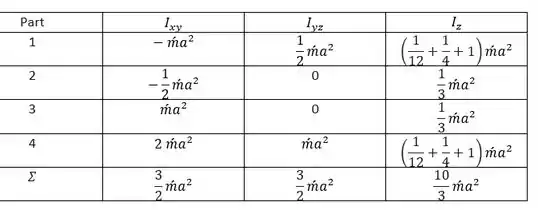
Passo 3

  1. Momento angular sobre B:

( H B ) x = - I x y ω = - 3 2   m ´ a 2 ω = - 3 2   0.06211 0.66667 2 8   π = - 1.04067   l b ∙ s ∙ f t

( H B ) y = - I y z ω = - 3 2   m ´ a 2 ω = - 3 2   0.06211 0.66667 2 8   π = 1.04067   l b ∙ s ∙ f t

( H B ) z = I z ω = 10 3   m ´ a 2 ω = 10 3   0.06211 0.66667 2 8   π = 2.3126   l b ∙ s ∙ f t

H B = 1.04067 2 + 1.04067 2 + 2.3126 2 = 2.7412   l b ∙ f t ∙ s

Passo 4

(b) Ângulo formado por H B   e eixo BA:

Vetor unitário ao longo do eixo BA:

λ = K

cos ⁡ θ = H B   ∙ λ H B = - 2.3126 2.7412 = 0.84365

Resposta

a) H B = - 1.041   l b ∙ f t ∙ s i + 1.041   l b ∙ f t ∙ s j + 2.31   l b ∙ f t ∙ s K

b) θ = 32.5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco fino de massa m = 4 kg gira com uma velocidade angular ω 2 em relação ao braço OA, que por sua vez gira com uma velocidade angular ω 1 em torno do eixo y. Determine (a) o binário M 1j , que po
18.46. Determine a energia cinética transmitida para o cubo do Problema 18.21.
18.45. Determine a energia cinética do corpo do Problema 18.19.
18.44. Determine a energia cinética da placa triangular do Problema 18.16
18.35. Os eixos de coordenadas mostrados na figura representam os eixos centroidais principais de inércia de uma sonda espacial de 1.500 kg cujos raios de giração são kx 0,4 m, ky 0,45 m e kz 0,375 m.