Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 79

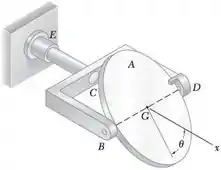
Um disco de 1,25 kg e 100 mm de raio está preso ao suporte BCD por meio de pequenos eixos montados em mancais em B e D. O suporte de 0,75 kg tem raio de giração de 75 mm em relação ao eixo x. Inicialmente, o conjunto está girando a 120 rpm com o disco no plano do suporte ( θ = 0). Se o disco for levemente deslocado e girar em relação ao suporte até θ = 90°, onde ele é contido por uma pequena barra em D, determine a velocidade angular final do conjunto.

Passo 1

O enunciado pede que a gente determine a velocidade angular final do conjunto.

Momento de inércia do suporte:

I C = m k C 2 = 1.5 32.2 3 12 2 = 2.9115   l b ∙ s 2 ∙ f t

Momento de inércia do disco:

θ = 0 :               I A = 1 4 m r 2

= 1 4 2.5 32.2 4 12 2 = 2.15666   l b ∙ s 2 ∙ f t

θ = 90 ° :               I A = 1 2 m r 2

= 1 2 2.5 32.2 4 12 2

= 4.3133   l b ∙ s 2 ∙ f t

Passo 2

Momento total de inércia sobre o eixo x:

θ = 0 :             I x 1 = I C + I A

= 5.0682 × 10 - 3   l b ∙ s 2 ∙ f t

θ = 90 ° :             I x 2 = I C + I A

= 7.2248 × 10 - 3   l b ∙ s 2 ∙ f t

Passo 3

Momento angular sobre o eixo x:

θ = 0 :             H 1 = I x 1 ω 2

= 5.0682 × 10 - 3   ω 1

θ = 90 :             H 2 = I x 2 ω 2

= 7.2248 × 10 - 3   ω 2

Passo 4

Conservação do momento angular.

H 1 = H 2 :               5.0682 × 10 - 3 ω 1 = 7.2248 × 10 - 3 ω 2

ω 2 = 0.7015 ω 1 = 0.7015 120   r p m

Resposta

ω 2 = 84.2   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para colocar um satélite de comunicações em uma órbita geossíncrona (ver Problema 12.80) a uma altitude de 35.580 km acima da superfície da Terra, o satélite primeiro é liberado do ônibus espacial, cu
Planos para a missão de um pouso não tripulado ao planeta Marte indica que o veículo de retorno à Terra primeiro descreve uma órbita circular a uma altitude dA × 2.200 km acima da superfície do planet
Um ônibus espacial S e um satélite A estão nas órbitas circulares mostradas na figura. Para poder recuperar o satélite, o ônibus espacial é primeiro colocado em uma trajetória elíptica BC, aumentando-
Uma bola A de 200 g e uma bola B de 400 g são montadas em umabarra horizontal que gira livremente sobre um eixo vertical. As bolassão mantidas nas posições mostradas na figura por pinos. O pino queseg
Uma pequena bola balança em um círculo horizontal na extremidade de uma corda de comprimento ∫ 1 , que forma um ângulo θ 1 com a vertical. A corda é então puxada lentamente pelo suporteem O até que o