Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 91

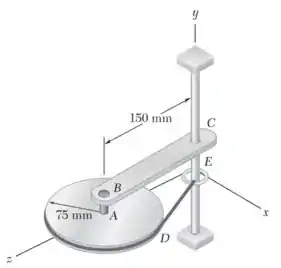
Um disco uniforme de 5 kg está ligado a uma haste uniforme BC de 3 kg por meio de um pino AB sem atrito. Uma corda elástica é enrolada em torno da borda do disco e é ligada a um anel em E. Tanto o anel E como a haste BC podem girar livremente em torno do eixo vertical.

Sabendo que o sistema é liberado a partir do repouso quando a tração na corda elástica é de 15 N, determine (a) a aceleração angular do disco, (b) a aceleração do centro do disco.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a aceleração angular do disco, (b) a aceleração do centro do disco., começamos então pela aceleração :D

Passo 2

(a)Aceleração Angular do Disco.

I _ d i s c o   = 1 2 m d i s c o   r 2

= 1 2 ( 5 k g ) ( 0.075 m ) 2   I _ d i s c o   = 14.06 × 10 - 3 k g ⋅ m 2

  + ) Σ M A = Σ M A e f f : ( 15 N ) ( 0.075 N ) =   1,125   N m                      

I → d i s c o   α d i s c o     1.125   N ∙ m = ( 14.06 × 10 3 k g ∙ m ² ) α d i s c o     α d i s c o   = 80.0 r a d / s 2          

Passo 3

(b)Aceleração do disco inteiro

Montagem inteira

I _ B C = 1 12 m B C ( B C ) 2 = 1 12 ( 3 k g ) ( 0.15 m ) 2 = 5.625 × 10 3 k g ⋅ m 2

Assumindo que

α B C   é   ) a A = ( 0.15 m ) α B C ↑   a _ = ( 0.075 m ) α B C  

+ ) Σ M C = Σ M C e f f : 0

  I d i s c o α d i s c o - m d i s c o a A ( 0.15 m ) - m B C a _ ( 0.075 m ) - I _ B C α B C   0

  = 14.06 × 10 - 3 k g ⋅ m 2 80 r a d / s 2 - ( 5 k g ) ( 0.15 m ) 2 α B C   - ( 3 k g ) ( 0.075 m ) 2 α B C - 5.625 × 10 3 k g ⋅ m 2 α B C   0

= 1.125 - 0.1125 α B C - 16.375 × 10 - 3 α B C - 5.625 × 10 - 3 α B C   0

= 1.125 - 0.135 α B C     a A = A C α B C = 0.15 m 8.333 r a d / s 2   a A = + 1.25 m / s ²      

α d i s c o = ( 80   r a d / s   ² ) j     a A = - ( 1.25 m / s ² ) i      

Resposta

a A = + 1.25 m / s ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma polia dupla está presa a um bloco deslizante por um pino em A. A polia interna, de 30m m de raio, está rigidamente presa à polia externa, de raio de 60m m . Sabendo que cada uma das cordas é puxad
Resolva o Problema 15.78, admitindo que a corda E seja puxada para cima a uma velocidade de 160 mm/s e que a corda F seja puxada para baixo a uma velocidade de 200 mm/s.
Um tambor de 75m m de raio está rigidamente preso a um tambor de 125m m de raio como ilustra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do
Um tambor de 75m m de raio está rigidamente preso a um tambor de 125m m de raio como ilustra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do
Usando o método da Seção 15.7, resolva o Problema 15.62.