Um tambor de freio de 150 mm é ligado a um volante de motor maior que não é mostrado na figura. O momento de inércia total da massa do tambor e do volante é 75 kg m2. Uma cinta de freio é utilizada para controlar o movimento do sistema e o coeficiente de atrito cinético entre a cinta e o tambor é 0,25. Sabendo que a força P de 100 N é aplicada quando a velocidade angular inicial do sistema é 240 rpm no sentido horário, determine o tempo requerido para o sistema parar. Mostre que o mesmo resultado é obtido se a velocidade angular inicial do sistema é 240 rpm no sentido anti-horário.
Passo 1
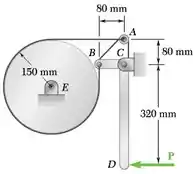
Alavanca ABCD
Equilíbrio estático:
Passo 2
Portanto, será ![]()
Passo 3
Fricção da correia:
Passo 4
Eq. (1):
Passo 5
Eq. (2):
Passo 6
Movimento uniformemente acelerado.
Nota: se ir invertido, TA e TB são trocados, não causando nenhuma alteração na Eq. (1) e Eq. (2). Assim, da Eq. (3), não é alterado.