Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 41

O disco possui uma velocidade angular constante p em torno de seu eixo z , e o garfo A possui uma velocidade angular constante ω 2 em torno de seu eixo, como mostrado. Simultaneamente, o conjunto inteiro gira em torno do eixo fixo X com uma velocidade angular constante ω 1 . Determine a expressão para a aceleração angular do disco quando o garfo o conduz para o plano vertical na posição mostrada. Resolva representando as variações vetoriais nas componentes da velocidade angular.

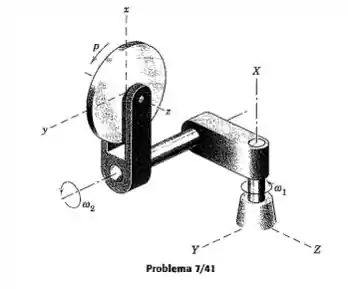
Passo 1

Para resolvermos a questão proposta iremos usar as relações de aceleração relativa considerando as componentes que ajudam no movimento do disco.

Passo 2

Temos que a aceleração do disco será a soma de todas as acelerações dos eixos. Temos que para ω 1 ⋅ i ^ , sua aceleração não implicará em mudança alguma para o movimento do disco e do eixo A. Portanto d ω 1 ⋅ i ^ d t = 0 .

Para os outros, temos que:

d ω 2 ⋅ j ^ d t = ω 2 ⋅ j ^ ˙ = ω 2 ⋅ Ω × j ^ = ω 1 ⋅ ω 2 ⋅ k ^

d p ⋅ k ^ d t = p ⋅ k ^ ˙ = p ⋅ Ω × k ^ = p ⋅ ω 2 ⋅ i ^ - p ⋅ ω 1 ⋅ j ^

Pois Ω = ω 1 ⋅ i ^ + ω 2 ⋅ j ^ + 0 ⋅ k ^

Portanto, temos que a aceleração será α = p ⋅ ω 2 ⋅ i ^ - p ⋅ ω 1 ⋅ j ^ + ω 1 ⋅ ω 2 ⋅ k ^

Resposta

Resposta: α = p ⋅ ω 2 ⋅ i ^ - p ⋅ ω 1 ⋅ j ^ + ω 1 ⋅ ω 2 ⋅ k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste vertical e o seu garfo vinculado giram em torno do eixo z na taxa constante Ω = 4r a d / s . Simultaneamente, a haste B gira em torno de seu eixo AO na taxa constante de w0 = 3 rad/s e o ângul
Enquanto manipula o haltere, as garras do dispositivo robótico possuem uma velocidade angular de 2 rad/s em torno do eixo OG com γ = 60 ° . Determine a aceleração angular do haltere. O conjunto inteir
O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c
A árvore AO da engrenagem cônica B gira em torno do eixo fixo O-x com uma velocidade constante N = 60 rpm na direção indicada. A engrenagem B se engrena com a engrenagem cônica C ao longo de seu cone
O guindaste possui uma lança de comprimento OP = 24 m e está girando em torno do eixo vertical na taxa constante de 2 rpm no sentido indicado. Simultaneamente, a lança está sendo abaixada na taxa cons