Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 115

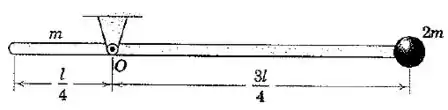
A haste delgada de massa m e comprimento l possui uma partícula (raio desprezível, massa 2 m ) presa a sua extremidade. Se o corpo é liberado a partir do repouso quando está na posição mostrada, determine a sua velocidade angular no instante em que passa pel posição vertical.

Passo 1

Vamos começar calculando o momento de inércia da haste em relação ao ponto O , em torno do qual o sistema vai girar.

Para isso vamos precisar do teorema dos eixos paralelos:

I O h a s t e = I c m + m d 2

I O h a s t e = 1 12 m l 2 + m l 4 2

I O h a s t e = 1 12 m l 2 + 1 16 m l 2

E agora vamos somar a isso o momento de inércia da massa presa na sua extremidade:

I O = 1 12 m l 2 + 1 16 m l 2 + 2 m 3 l 4 2

I O = 61 48 m l 2

Passo 2

Agora vamos aplicar a lei de conservação de energia entre dois instantes: o ponto de partida e o instante em que a haste pela posição vertical.

T 1 + V 1 = T 2 + V 2

Como o sistema parte do repouso, temos T 1 = 0 :

V 1 = T 2 + V 2

E vamos definir o zero da energia potencial como a altura do ponto O , então V 1 = 0 :

0 = T 2 + V 2

Quando a barra estiver na vertical, a massa 2 m estará a uma altura 3 l 4 abaixo do ponto O , e o centro de massa da haste estará a uma altura l 4 abaixo do ponto O então:

V 2 = - m g 2 3 l 4 + l 4 = - 7 4 m g l

Então:

T 2 = 7 4 m g l

1 2 I ω 2 = 7 4 m g l

1 2 61 48 m l 2 ω 2 = 7 4 m g l

ω 2 = ( 7 ) ( 48 ) ( 2 ) ( 4 ) ( 61 ) g l

ω = 1,660   g l

Resposta

A sua velocidade angular será ω = 1,660   g / l .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bobina tem uma massa de 100 kg e raio de giração de 400 mm em relação a seu centro de massa O. Se ela é liberada do repouso, determine sua velocidade angular após seu centro O haver descido pelo pla
O cilindro A, de 25 kg, está descendo a uma velocidade de 6 m/s quando o freio é acionado. Se a roda B deve ser parada após haver girado cinco revoluções, determine a força constante P, que deve ser a
A bobina tem uma massa de 60k g e raio de giração k G = 0,3m . Se ela é liberada do repouso, determine a que distância seu centro desce pelo plano liso, antes de atingir uma velocidade angular de ω =
O tambor tem massa de 50k g e raio de giração em relação ao pino em O , k O = 0,23m . Se o bloco de 15k g desloca-se para baixo a 3m / s , e uma força P = 100N é aplicada à alavanca do freio, determin
Um homem com massa de 90k g está sentado em uma cadeira da roda-gigante, a qual, excluindo-se o homem tem massa de 7500k g e raio de giração k O = 11,1m . Se um torque M = 120 10 3N ⋅ m é aplicado em