Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 42
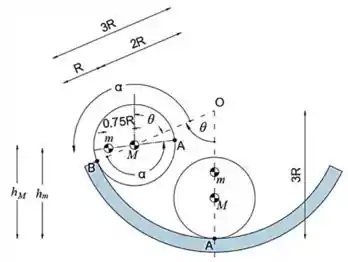
O cilindro de massa M e raio R rola sem deslizar na superfície circular de raio 3R. Preso ao cilindro está um pequeno corpo de massa m. Determine a relação necessária entre M e m se o corpo deve ser estável na posição de equilíbrio mostrada.
Passo 1
O enunciado pede que a gente determine a relação necessária entre M e m se o corpo deve ser estável na posição de equilíbrio mostrada.
Observe que não há forças externas agindo nem molas ligadas ao sistema, portanto, podemos escrever a equação de equilíbrio como
(1)
Passo 2
Observe que a rotação total do cilindro é a, e que podemos escrever o comprimento do arco (AB) ̂ tanto como arco de círculo de raio 3R com ângulo θ, quanto como círculo de raio R com ângulo α
Em seguida, a partir do esboço, podemos ver que as alturas hM e hm são
Podemos substituir α por 3θ para obter
Passo 3
Você pode notar que no cilindro esquerdo o centro de massa m está abaixo do centro de massa M, enquanto em nossa equação há um sinal -, porque nossa equação é escrita como função de θ, e para θ = 0 o centro de massa m é acima de M, o
o sinal se tornará + quando 2θ> 90°
Passo 4
Uma vez que temos duas massas aqui, podemos escrever a expressão para a energia potencial gravitacional como
substituiremos por e by
Derive ambos lados da equação para obter
Passo 5
A seguir, substituiremos δVg pela expressão (2) na equação de equilíbrio (1)
Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero
Podemos dividir os dois lados da equação por gR
(3)
Passo 6
Para verificar a estabilidade da posição θ = 0, vamos simplesmente colocar o valor de θ em (3)
A partir daqui, podemos escrever a relação entre as massas M e m necessárias para garantir a estabilidade