Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 8

Represente graficamente os diagramas de força cortante e momento fletor para o tubo. A extremidade rosqueada está sujeita a uma força horizontal de 5 kN. Dica: As reações no pino C devem ser substituídas por cargas equivalentes no ponto B no eixo do tubo.

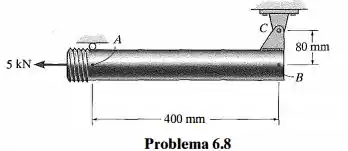
Passo 1

Vamos fazer o diagrama de corpo livre:

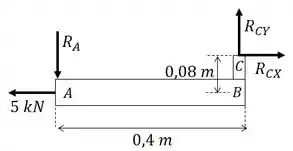
Fazemos o somatório de forças:

∑ F x = 0 ⇒ - 5 k N + R C X = 0

R C X = 5   k N

∑ M C = 0 ⇒ - 5 ⋅ 0,08 + R A ⋅ 0,4 = 0

R A = 1 k N

∑ F y = 0 ⇒ - R A + R C Y = 0

R C Y = 1   k N

Passo 2

Vamos remover as forças em C e substituí-las por forças equivalente em B

- 5 ⋅ 0,08 + M B = 0

M B = 0,4   k N m

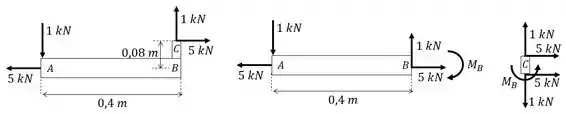
Passo 3

Vamos fazer uma seção entre A B e estudar os esforços interno:

∑ F x = 0 ⇒ - 5 k N + N ( x ) = 0

N ( x ) = 5   k N

∑ F y = 0 ⇒ - 1 - V ( x ) = 0

V x = - 1   k N

∑ M C = 0 ⇒ 1 ⋅ x + M ( x ) = 0

M x = - x

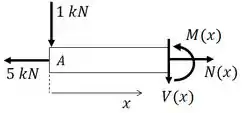
Agora temos as equações de Esforço Normal Interno, Esforço Cortante e Momento Fletor

Equações de esforço interno = N ( x ) = 5   k N V x = - 1   k N M x = - x

Passo 4

Utilizamos as equações para gerar os gráficos de esforço cortante e momento fletor

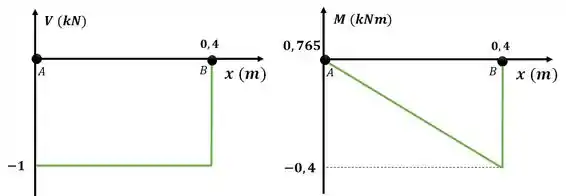
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elemento diferencial tomado de uma barra curva é mostrado na figura. Mostre que d n d θ = V ; d V d θ = N ; d M d θ =- T e d T d θ = M . dM/dθ
O cano tem massa de 12 kg/m e está preso à parede em A. Determine as cargas internas resultantes que agem na seção transversal que passa por B.
A haste do parafuso está sujeita a uma tensão de 400 N. Determine as cargas internas resultantes que agem na seção transversal no ponto C.
O eixo está apoiado em suas extremidades por dois mancais A e B e está sujeito às iorças aplicadas às polias nele fixadas. Determine as cargas internas resultantes que agem na seção transversal que pa
Determine as cargas internas resultantes que agem na seção transversal da estrutura nos pontos F e G . O contato em E é liso.