Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 77
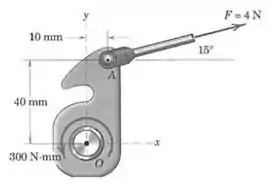
O dispositivo mostrado é uma peça de um mecanismo de liberação do encosto de um banco de automóvel. A peça é submetida a uma força de exercida em e um momento de exercido por uma mola de torção escondida. Determine a interseção com o eixo da linha de ação da força única equivalente.
Passo 1
Vamos começar calculando o momento total em relação ao ponto :
Onde é o momento de que temos inicialmente, e é o momento da força em relação a .
Para calcular , vamos calcular o momento de cada componente da força separadamente:
E o sinal negativo aparece em porque essa componente da força favorece a rotação no sentido contrário ao de , que nós adotamos como positivo.
E agora podemos calcular o momento total:
Passo 2
Beleza, agora queremos substituir essas forças e momentos por uma única força, que tenha exatamenteo mesmo efeito.
Para que a força resultante seja a mesma, vamos smplesmente manter o mesmo vetor , e vamos apenas alterar sua posição para gerar o mesmo momento que tínhamos antes.
Como nosso momento original favorecia a rotação no sentido antio-horário, vamos posicionar nossa força ao longo do eixo , em algum lugar abaixo do ponto :
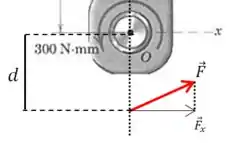
E como estamos abaixo da origem do nosso sistema de coordenadas:
Resposta
A interseção acontece em .