138. Determine a intensidade e a direção da resultante F x = F 1 + F 2 + F 3 das três forças encontrando primeiro a resultante F ' = F 1 + F 3 e, depois, formando F R = F ' + F 2 . Especifique sua direção medida no sentido anti-horário a partir do eixo x positivo.

A intensidade da força é: 177,6N O ângulo que da a direção é: θ = 85,2 °

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 138

138. Determine a intensidade e a direção da resultante das três forças encontrando primeiro a resultante e, depois, formando . Especifique sua direção medida no sentido anti-horário a partir do eixo positivo.

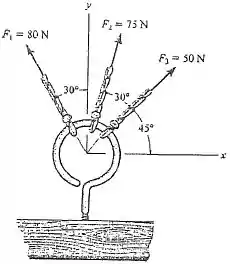
Passo 1

Vamos somar as forças através da soma das suas componentes. Vamos decompor cada força em suas componentes e , depois somar a componente de cada força e depois somar a componente .

Passo 2

Vamos decompor as forças.

Passo 3

Agora vamos somar componente a componente dos vetores, a soma será realizada na ordem que o enunciado pede, então:

Agora vamos fazer:

Para achar a intensidade basta calcular o modulo do vetor :

Passo 4

Quando enunciado disse para especificar a direção medida no sentido anti-horário a partir do eixo positivo, isso nada mais é que da direção do vetor usando o ângulo que ele faz com eixo .

Para calcular esse ângulo vamos usar as componentes da da seguinte maneira:

Onde:

Então:

Resposta

A intensidade da força é:

O ângulo que da a direção é:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois binários atuam sobre a estrutura. Se o momento de binário resultante deve ser zero, determine a distância d entre as forças do binário de 500N .

As forças e binários mostrados na figura são aplicados em dois parafusos à medida que uma chapa metálica é parafusada em um bloco de madeira. Reduza as forças e os binários a um torsor equivalente e d

Resolva o Problema 3.131 em caso dos estudantes quiserem colocar o limite de peso na quarta caixa e pelo menos um lado da caixa deva coincidir com um lado do reboque.

Quatro placas são montadas numa estrutura no vão da autoestrada, e as intensidades das forças do vento horizontal exercidas nas placas são mostradas na figura. Determine a e b tal que o ponto de aplic

Três forças de uma mesma intensidade P atuam no cubo de lado a como mostrado na figura. Substiua as três forças por um torsor equivalente e determine a a intensidade, a direção e o sentido da resultan